22.(8分)如图,在直角坐标系中,一次函数$y_{1}=kx + b$的图象与反比例函数$y_{2}=\frac{m}{x}(m>0)$的图象交于点$A(1,2)$,$B(n,-1)$。
(1)求两个函数的解析式;
(2)根据图象,直接写出关于$x$的不等式$kx + b\leqslant\frac{m}{x}$的解集;
(3)若$P$为$y$轴上的一个动点,$Q$为双曲线上的一个动点,当以$A$,$B$,$P$,$Q$为顶点的四边形是平行四边形时,求点$P$的坐标。

(1)求两个函数的解析式;
(2)根据图象,直接写出关于$x$的不等式$kx + b\leqslant\frac{m}{x}$的解集;
(3)若$P$为$y$轴上的一个动点,$Q$为双曲线上的一个动点,当以$A$,$B$,$P$,$Q$为顶点的四边形是平行四边形时,求点$P$的坐标。

答案:
(1)把$A(1,2)$代入$y_{2}=\frac{m}{x}(m > 0)$,得$m = 2$,所以反比例函数的解析式为$y_{2}=\frac{2}{x}$。把$B(n,-1)$代入$y_{2}=\frac{2}{x}$,得$-1=\frac{2}{n}$。所以$n=-2$。所以$B(-2,-1)$。因为一次函数$y_{1}=kx + b$的图象过点$A(1,2)$,$B(-2,-1)$,所以$\begin{cases}k + b = 2\\-2k + b = -1\end{cases}$,解得$\begin{cases}k = 1\\b = 1\end{cases}$。所以一次函数的解析式为$y_{1}=x + 1$ (2)由图象,可知关于$x$的不等式$kx + b\leqslant\frac{m}{x}$的解集是$x\leqslant -2$或$0 < x\leqslant1$ (3)因为$P$为$y$轴上的一个动点,$Q$为双曲线上的一个动点,所以设$P(0,a)$,$Q(c,\frac{2}{c})$。因为以$A$,$B$,$P$,$Q$为顶点的四边形是平行四边形,所以当以$AP$为对角线时,由中点坐标公式,得$\begin{cases}1=-2 + c\\2 + a=-1+\frac{2}{c}\end{cases}$,解得$\begin{cases}a=-\frac{7}{3}\\c = 3\end{cases}$,所以$P(0,-\frac{7}{3})$。当以$AQ$为对角线时,由中点坐标公式,得$\begin{cases}1 + c=-2\\2+\frac{2}{c}=-1 + a\end{cases}$,解得$\begin{cases}a=\frac{7}{3}\\c=-3\end{cases}$,所以$P(0,\frac{7}{3})$。当以$AB$为对角线时,由中点坐标公式,得$\begin{cases}1-2 = c\\2-1=a+\frac{2}{c}\end{cases}$,解得$\begin{cases}a = 3\\c=-1\end{cases}$,所以$P(0,3)$。综上所述,点$P$的坐标为$(0,-\frac{7}{3})$或$(0,\frac{7}{3})$或$(0,3)$
23.(8分)如图,等边三角形$ABC$的边长为6,$P$,$D$分别是边$BC$,$AC$上的点,且$\angle APD = 60^{\circ}$,$BP = 2$,求$CD$的长。
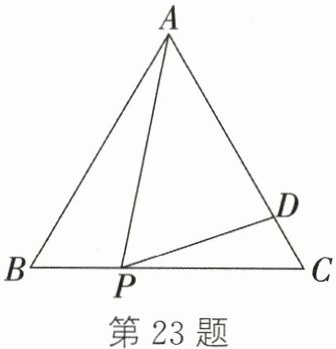

答案:
因为$\triangle ABC$是等边三角形,所以$\angle B=\angle C = 60^{\circ}$,$AB = BC = 6$。所以$\angle BAP+\angle BPA = 120^{\circ}$。因为$\angle APD = 60^{\circ}$,所以$\angle BPA+\angle CPD = 120^{\circ}$。所以$\angle BAP=\angle CPD$。所以$\triangle ABP\sim\triangle PCD$。所以$\frac{AB}{PC}=\frac{BP}{CD}$。因为$PC = BC - BP = 6 - 2 = 4$,所以$\frac{6}{4}=\frac{2}{CD}$。所以$CD=\frac{4}{3}$
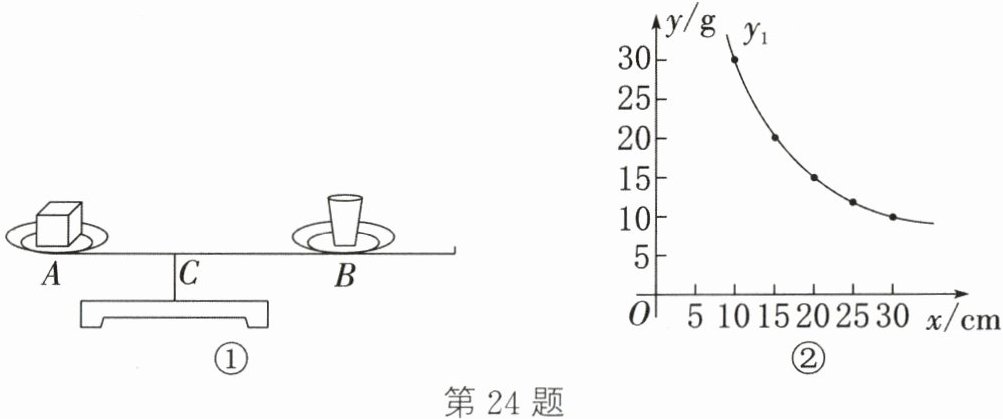
24.(10分)在实验课上,小明做了一个实验。如图①,在仪器左边托盘$A$(固定)中放置一个物体,在右边托盘$B$(可左右移动)中放置一个可以装水的容器,容器的质量为5 g。在容器中加入一定质量的水,可以使仪器左右平衡。改变托盘$B$与点$C$之间的距离$x$(单位:$cm$)($0<x\leqslant60$),记录容器中加入的水的质量,得到下表:
|托盘$B$与点$C$之间的距离$x/cm$|30|25|20|15|10|
|----|----|----|----|----|----|
|容器与水的总质量$y_{1}/g$|10|12|15|20|30|
|加入的水的质量$y_{2}/g$|5|7|10|15|25|
把上表中的$x$与$y_{1}$各组对应值作为点的坐标,在直角坐标系中描出这些点,并用光滑的曲线连接起来,得到如图②所示的$y_{1}$关于$x$的函数图象。
(1)请在该直角坐标系中作出$y_{2}$关于$x$的函数图象。
(2)观察函数图象,并结合表中的数据:
① 猜测$y_{1}$与$x$之间的函数关系,并求$y_{1}$关于$x$的函数解析式;
② 求$y_{2}$关于$x$的函数解析式;
③ 当$0<x\leqslant60$时,$y_{1}$随$x$的增大而_______(填“增大”或“减小”),$y_{2}$随$x$的增大而_______(填“增大”或“减小”),函数$y_{2}$的图象可以由函数$y_{1}$的图象向_______(填“上”“下”“左”或“右”)平移得到。
(3)若在容器中加入的水的质量$y_{2}$(单位:$g$)满足$19\leqslant y_{2}\leqslant45$,求$x$的取值范围。
|托盘$B$与点$C$之间的距离$x/cm$|30|25|20|15|10|
|----|----|----|----|----|----|
|容器与水的总质量$y_{1}/g$|10|12|15|20|30|
|加入的水的质量$y_{2}/g$|5|7|10|15|25|
把上表中的$x$与$y_{1}$各组对应值作为点的坐标,在直角坐标系中描出这些点,并用光滑的曲线连接起来,得到如图②所示的$y_{1}$关于$x$的函数图象。
(1)请在该直角坐标系中作出$y_{2}$关于$x$的函数图象。
(2)观察函数图象,并结合表中的数据:
① 猜测$y_{1}$与$x$之间的函数关系,并求$y_{1}$关于$x$的函数解析式;
② 求$y_{2}$关于$x$的函数解析式;
③ 当$0<x\leqslant60$时,$y_{1}$随$x$的增大而_______(填“增大”或“减小”),$y_{2}$随$x$的增大而_______(填“增大”或“减小”),函数$y_{2}$的图象可以由函数$y_{1}$的图象向_______(填“上”“下”“左”或“右”)平移得到。
(3)若在容器中加入的水的质量$y_{2}$(单位:$g$)满足$19\leqslant y_{2}\leqslant45$,求$x$的取值范围。

答案:
(1)如图,$y_{2}$关于$x$的函数图象即为所求 (2)①$y_{1}$是$x$的反比例函数 设$y_{1}=\frac{k}{x}(k\neq0)$。把$(30,10)$代入,得$10=\frac{k}{30}$,解得$k = 300$。所以$y_{1}$关于$x$的函数解析式为$y_{1}=\frac{300}{x}(0 < x\leqslant60)$ ②因为$y_{1}=y_{2}+5$,所以$y_{2}+5=\frac{300}{x}$。所以$y_{2}$关于$x$的函数解析式为$y_{2}=\frac{300}{x}-5(0 < x\leqslant60)$ ③减小 减小 下 (3)因为$y_{2}=\frac{300}{x}-5$,$19\leqslant y_{2}\leqslant45$,所以$19\leqslant\frac{300}{x}-5\leqslant45$。所以$24\leqslant\frac{300}{x}\leqslant50$,解得$6\leqslant x\leqslant12.5$
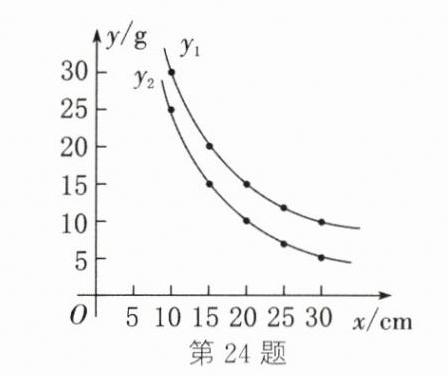
(1)如图,$y_{2}$关于$x$的函数图象即为所求 (2)①$y_{1}$是$x$的反比例函数 设$y_{1}=\frac{k}{x}(k\neq0)$。把$(30,10)$代入,得$10=\frac{k}{30}$,解得$k = 300$。所以$y_{1}$关于$x$的函数解析式为$y_{1}=\frac{300}{x}(0 < x\leqslant60)$ ②因为$y_{1}=y_{2}+5$,所以$y_{2}+5=\frac{300}{x}$。所以$y_{2}$关于$x$的函数解析式为$y_{2}=\frac{300}{x}-5(0 < x\leqslant60)$ ③减小 减小 下 (3)因为$y_{2}=\frac{300}{x}-5$,$19\leqslant y_{2}\leqslant45$,所以$19\leqslant\frac{300}{x}-5\leqslant45$。所以$24\leqslant\frac{300}{x}\leqslant50$,解得$6\leqslant x\leqslant12.5$

查看更多完整答案,请扫码查看


