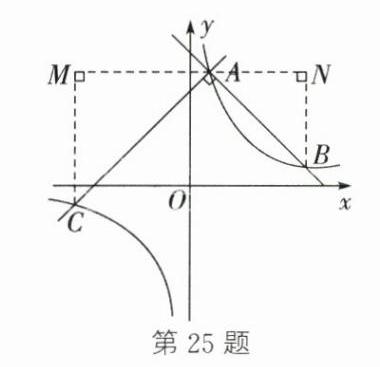
25.(10分)如图,直线$y = -x + 7$与反比例函数$y = \frac{k}{x}$的图象交于点$A(1,m)$和点$B$。
(1)求$m$,$k$的值。
(2)若直线$AC\perp AB$,交反比例函数$y = \frac{k}{x}$的图象于第三象限的点$C$,求点$C$的坐标。
(3)在(2)的条件下,在$y$轴上是否存在点$D$,使$\angle BDC = 90^{\circ}$?若存在,求出点$D$的坐标;若不存在,请说明理由。

(1)求$m$,$k$的值。
(2)若直线$AC\perp AB$,交反比例函数$y = \frac{k}{x}$的图象于第三象限的点$C$,求点$C$的坐标。
(3)在(2)的条件下,在$y$轴上是否存在点$D$,使$\angle BDC = 90^{\circ}$?若存在,求出点$D$的坐标;若不存在,请说明理由。

答案:
(1)将$A(1,m)$代入$y=-x + 7$,得$m = 6$,所以点$A$的坐标为$(1,6)$。将$A(1,6)$代入$y=\frac{k}{x}$,得$k = 6$ (2)由(1),得反比例函数的解析式为$y=\frac{6}{x}$。当$-x + 7=\frac{6}{x}$时,$x = 1$或$x = 6$。在$y=\frac{6}{x}$中,当$x = 6$时,$y = 1$,所以点$B$的坐标为$(6,1)$。如图,过点$A$作$MN// x$轴,过点$C$作$CM\perp MN$于点$M$,过点$B$作$BN\perp MN$于点$N$,则$\angle M=\angle N = 90^{\circ}$。因为$AC\perp AB$,所以$\angle BAC = 90^{\circ}$。所以$\angle BAN+\angle CAM = 90^{\circ}$。因为$\angle N = 90^{\circ}$,所以$\angle BAN+\angle ABN = 90^{\circ}$。所以$\angle CAM=\angle ABN$。所以$\triangle ABN\sim\triangle CAM$。所以$\frac{AN}{CM}=\frac{BN}{AM}$。设点$C$的坐标为$(t,\frac{6}{t})$。因为$x_{B}=x_{N}=6$,$x_{A}=1$,所以$AN = 5$。因为$x_{C}=x_{M}=t$,所以$AM = 1 - t$。因为$y_{A}=y_{N}=6$,$y_{B}=1$,所以$BN = 5$。因为$y_{M}=y_{A}=6$,$y_{C}=\frac{6}{t}$,所以$CM = 6-\frac{6}{t}$。所以$\frac{5}{6-\frac{6}{t}}=\frac{5}{1 - t}$,解得$t_{1}=1$(增根,舍去),$t_{2}=-6$。所以点$C$的坐标为$(-6,-1)$ (3)存在 因为$B(6,1)$,$C(-6,-1)$,所以点$B$与点$C$关于原点对称。所以连接$BC$,$BC$必过点$O$。所以$OB=\frac{1}{2}BC$。当$\angle BDC = 90^{\circ}$时,$OD=\frac{1}{2}BC = OB$,所以$OD=OB=\sqrt{6^{2}+1^{2}}=\sqrt{37}$。所以点$D$的坐标为$(0,-\sqrt{37})$或$(0,\sqrt{37})$
(1)将$A(1,m)$代入$y=-x + 7$,得$m = 6$,所以点$A$的坐标为$(1,6)$。将$A(1,6)$代入$y=\frac{k}{x}$,得$k = 6$ (2)由(1),得反比例函数的解析式为$y=\frac{6}{x}$。当$-x + 7=\frac{6}{x}$时,$x = 1$或$x = 6$。在$y=\frac{6}{x}$中,当$x = 6$时,$y = 1$,所以点$B$的坐标为$(6,1)$。如图,过点$A$作$MN// x$轴,过点$C$作$CM\perp MN$于点$M$,过点$B$作$BN\perp MN$于点$N$,则$\angle M=\angle N = 90^{\circ}$。因为$AC\perp AB$,所以$\angle BAC = 90^{\circ}$。所以$\angle BAN+\angle CAM = 90^{\circ}$。因为$\angle N = 90^{\circ}$,所以$\angle BAN+\angle ABN = 90^{\circ}$。所以$\angle CAM=\angle ABN$。所以$\triangle ABN\sim\triangle CAM$。所以$\frac{AN}{CM}=\frac{BN}{AM}$。设点$C$的坐标为$(t,\frac{6}{t})$。因为$x_{B}=x_{N}=6$,$x_{A}=1$,所以$AN = 5$。因为$x_{C}=x_{M}=t$,所以$AM = 1 - t$。因为$y_{A}=y_{N}=6$,$y_{B}=1$,所以$BN = 5$。因为$y_{M}=y_{A}=6$,$y_{C}=\frac{6}{t}$,所以$CM = 6-\frac{6}{t}$。所以$\frac{5}{6-\frac{6}{t}}=\frac{5}{1 - t}$,解得$t_{1}=1$(增根,舍去),$t_{2}=-6$。所以点$C$的坐标为$(-6,-1)$ (3)存在 因为$B(6,1)$,$C(-6,-1)$,所以点$B$与点$C$关于原点对称。所以连接$BC$,$BC$必过点$O$。所以$OB=\frac{1}{2}BC$。当$\angle BDC = 90^{\circ}$时,$OD=\frac{1}{2}BC = OB$,所以$OD=OB=\sqrt{6^{2}+1^{2}}=\sqrt{37}$。所以点$D$的坐标为$(0,-\sqrt{37})$或$(0,\sqrt{37})$

查看更多完整答案,请扫码查看


