22. (12分)如图,在△ABC中,∠ACB = 90°,CD是边AB上的高,BE平分∠ABC,BE分别与AC,CD相交于点E,F.
(1) 求证:△AEB∽△CFB;
(2) 求证:$\frac{AE}{CE}=\frac{AB}{CB}$;
(3) 若CE = 5,EF = 2$\sqrt{5}$,BD = 6,求AD的长.

(1) 求证:△AEB∽△CFB;
(2) 求证:$\frac{AE}{CE}=\frac{AB}{CB}$;
(3) 若CE = 5,EF = 2$\sqrt{5}$,BD = 6,求AD的长.

答案:
(1)
∵ $\angle ACB = 90^{\circ}$,
∴ $\angle ACD+\angle BCD = 90^{\circ}$。
∵ $CD$是$\triangle ABC$的高,
∴ $CD\perp AB$。
∴ $\angle ADC = 90^{\circ}$。
∴ $\angle A+\angle ACD = 90^{\circ}$。
∴ $\angle A=\angle BCD$。
∵ $BE$平分$\angle ABC$,
∴ $\angle ABE=\angle CBF$。
∴ $\triangle AEB\sim\triangle CFB$
(2)
∵ $\angle ABE=\angle CBE$,$\angle A=\angle BCD$,
∴ $\angle CFE=\angle BCD+\angle CBE=\angle A+\angle ABE=\angle CEF$。
∴ $CE = CF$。
∵ $\triangle AEB\sim\triangle CFB$,
∴ $\frac{AE}{CF}=\frac{AB}{CB}$。
∴ $\frac{AE}{CE}=\frac{AB}{CB}$
(3) 如图,过点$C$作$CH\perp EF$于点$H$。
∵ $CE = CF$,$CE = 5$,$CH\perp EF$,$EF = 2\sqrt{5}$,
∴ $EH = FH=\frac{1}{2}EF=\sqrt{5}$,$CF = 5$。
∴ 在$Rt\triangle CHE$中,由勾股定理,得$CH=\sqrt{CE^{2}-EH^{2}}=\sqrt{5^{2}-(\sqrt{5})^{2}}=2\sqrt{5}$。
∵ $CD\perp AB$,$CH\perp EF$,
∴ $\angle BDF=\angle CHF = 90^{\circ}$。又
∵ $\angle BFD=\angle CFH$,
∴ $\triangle BFD\sim\triangle CFH$。
∴ $\frac{DF}{HF}=\frac{BD}{CH}$,即$\frac{DF}{\sqrt{5}}=\frac{6}{2\sqrt{5}}$。
∴ $DF = 3$。
∴ $CD = CF + DF = 8$。
∵ $\angle A=\angle BCD$,$\angle ADC=\angle CDB = 90^{\circ}$,
∴ $\triangle ACD\sim\triangle CBD$。
∴ $\frac{AD}{CD}=\frac{CD}{BD}$,即$\frac{AD}{8}=\frac{8}{6}$。
∴ $AD=\frac{32}{3}$
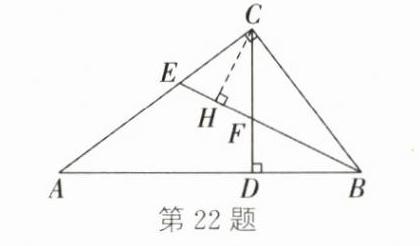
(1)
∵ $\angle ACB = 90^{\circ}$,
∴ $\angle ACD+\angle BCD = 90^{\circ}$。
∵ $CD$是$\triangle ABC$的高,
∴ $CD\perp AB$。
∴ $\angle ADC = 90^{\circ}$。
∴ $\angle A+\angle ACD = 90^{\circ}$。
∴ $\angle A=\angle BCD$。
∵ $BE$平分$\angle ABC$,
∴ $\angle ABE=\angle CBF$。
∴ $\triangle AEB\sim\triangle CFB$
(2)
∵ $\angle ABE=\angle CBE$,$\angle A=\angle BCD$,
∴ $\angle CFE=\angle BCD+\angle CBE=\angle A+\angle ABE=\angle CEF$。
∴ $CE = CF$。
∵ $\triangle AEB\sim\triangle CFB$,
∴ $\frac{AE}{CF}=\frac{AB}{CB}$。
∴ $\frac{AE}{CE}=\frac{AB}{CB}$
(3) 如图,过点$C$作$CH\perp EF$于点$H$。
∵ $CE = CF$,$CE = 5$,$CH\perp EF$,$EF = 2\sqrt{5}$,
∴ $EH = FH=\frac{1}{2}EF=\sqrt{5}$,$CF = 5$。
∴ 在$Rt\triangle CHE$中,由勾股定理,得$CH=\sqrt{CE^{2}-EH^{2}}=\sqrt{5^{2}-(\sqrt{5})^{2}}=2\sqrt{5}$。
∵ $CD\perp AB$,$CH\perp EF$,
∴ $\angle BDF=\angle CHF = 90^{\circ}$。又
∵ $\angle BFD=\angle CFH$,
∴ $\triangle BFD\sim\triangle CFH$。
∴ $\frac{DF}{HF}=\frac{BD}{CH}$,即$\frac{DF}{\sqrt{5}}=\frac{6}{2\sqrt{5}}$。
∴ $DF = 3$。
∴ $CD = CF + DF = 8$。
∵ $\angle A=\angle BCD$,$\angle ADC=\angle CDB = 90^{\circ}$,
∴ $\triangle ACD\sim\triangle CBD$。
∴ $\frac{AD}{CD}=\frac{CD}{BD}$,即$\frac{AD}{8}=\frac{8}{6}$。
∴ $AD=\frac{32}{3}$

23. (12分)(扬州中考)如图,点A,B,M,E,F依次在直线l上,点A,B固定不动,且AB = 2,分别以AB,EF为边在直线l同侧作正方形ABCD,正方形EFGH,∠PMN = 90°,直角边MP恒过点C,直角边MN恒过点H.
(1) 如图①,若BE = 10,EF = 12,求点M与点B之间的距离;
(2) 如图①,若BE = 10,当点M在点B,E之间运动时,求EH长的最大值;
(3) 如图②,若BF = 22,当点E在点B,F之间运动时,点M随之运动,连接CH,O是CH的中点,连接HB,MO,则2OM + HB的最小值为_______.

(1) 如图①,若BE = 10,EF = 12,求点M与点B之间的距离;
(2) 如图①,若BE = 10,当点M在点B,E之间运动时,求EH长的最大值;
(3) 如图②,若BF = 22,当点E在点B,F之间运动时,点M随之运动,连接CH,O是CH的中点,连接HB,MO,则2OM + HB的最小值为_______.

答案:
(1)
∵ 四边形$ABCD$和四边形$EFGH$都是正方形,
∴ $AB = BC = 2$,$EH = EF = 12$,$\angle CBA=\angle HEF = 90^{\circ}$。
∴ $\angle CBM=\angle MEH = 90^{\circ}$。
∵ $\angle PMN = 90^{\circ}$,
∴ $\angle CMB+\angle BCM=\angle CMB+\angle EMH = 90^{\circ}$。
∴ $\angle BCM=\angle EMH$。
∴ $\triangle MCB\sim\triangle HME$。
∴ $\frac{BC}{EM}=\frac{BM}{EH}$。
∴ $\frac{2}{10 - BM}=\frac{BM}{12}$,解得$BM = 4$或6。
∴ 点$M$与点$B$之间的距离是4或6
(2) 由
(1),知$\frac{BC}{EM}=\frac{BM}{EH}$,设$EH = y$,$BM = x$。
∵ $BE = 10$,
∴ $EM = 10 - x$。
∴ $\frac{2}{10 - x}=\frac{x}{y}$。
∴ $y=-\frac{1}{2}x^{2}+5x=-\frac{1}{2}(x - 5)^{2}+12.5$。
∵ $-\frac{1}{2}<0$,
∴ 当$x = 5$时,$y$取最大值12.5,即$EH$长的最大值为12.5
(3) $2\sqrt{221}$ 解析:
∵ $\angle CMH = 90^{\circ}$,$O$是$CH$的中点,
∴ $CH = 2OM$。
∴ $2OM + HB = CH + HB$。如图,连接$FH$,作点$B$关于$FH$的对称点$B'$,连接$B'C$交直线$FH$于点$H'$,则当点$H$在点$H'$处时,$B'C$的长即为$CH + HB$的最小值。过点$C$作$CQ\perp B'F$于点$Q$。
∵ $FH$是正方形$EFGH$的对角线,
∴ $\angle BFH=\angle B'FH = 45^{\circ}$。易得点$B'$在$FG$的延长线上。
∵ 四边形$ABCD$和四边形$EFGH$都是正方形,
∴ $\angle ABC = 90^{\circ}$,$\angle BFQ = 90^{\circ}$。
∴ $\angle CBF=\angle BFQ=\angle FQC = 90^{\circ}$。
∴ 四边形$CBFQ$为矩形。
∴ $FQ = BC = 2$,$CQ = BF = 22$。由对称,得$BF = B'F = 22$,
∴ $B'Q = B'F - QF = 20$。在$Rt\triangle B'CQ$中,由勾股定理,得$B'C^{2}=\sqrt{CQ^{2}+B'Q^{2}}=2\sqrt{221}$,即$CH + HB$的最小值为$2\sqrt{221}$。
∴ $2OM + HB$的最小值为$2\sqrt{221}$。

(1)
∵ 四边形$ABCD$和四边形$EFGH$都是正方形,
∴ $AB = BC = 2$,$EH = EF = 12$,$\angle CBA=\angle HEF = 90^{\circ}$。
∴ $\angle CBM=\angle MEH = 90^{\circ}$。
∵ $\angle PMN = 90^{\circ}$,
∴ $\angle CMB+\angle BCM=\angle CMB+\angle EMH = 90^{\circ}$。
∴ $\angle BCM=\angle EMH$。
∴ $\triangle MCB\sim\triangle HME$。
∴ $\frac{BC}{EM}=\frac{BM}{EH}$。
∴ $\frac{2}{10 - BM}=\frac{BM}{12}$,解得$BM = 4$或6。
∴ 点$M$与点$B$之间的距离是4或6
(2) 由
(1),知$\frac{BC}{EM}=\frac{BM}{EH}$,设$EH = y$,$BM = x$。
∵ $BE = 10$,
∴ $EM = 10 - x$。
∴ $\frac{2}{10 - x}=\frac{x}{y}$。
∴ $y=-\frac{1}{2}x^{2}+5x=-\frac{1}{2}(x - 5)^{2}+12.5$。
∵ $-\frac{1}{2}<0$,
∴ 当$x = 5$时,$y$取最大值12.5,即$EH$长的最大值为12.5
(3) $2\sqrt{221}$ 解析:
∵ $\angle CMH = 90^{\circ}$,$O$是$CH$的中点,
∴ $CH = 2OM$。
∴ $2OM + HB = CH + HB$。如图,连接$FH$,作点$B$关于$FH$的对称点$B'$,连接$B'C$交直线$FH$于点$H'$,则当点$H$在点$H'$处时,$B'C$的长即为$CH + HB$的最小值。过点$C$作$CQ\perp B'F$于点$Q$。
∵ $FH$是正方形$EFGH$的对角线,
∴ $\angle BFH=\angle B'FH = 45^{\circ}$。易得点$B'$在$FG$的延长线上。
∵ 四边形$ABCD$和四边形$EFGH$都是正方形,
∴ $\angle ABC = 90^{\circ}$,$\angle BFQ = 90^{\circ}$。
∴ $\angle CBF=\angle BFQ=\angle FQC = 90^{\circ}$。
∴ 四边形$CBFQ$为矩形。
∴ $FQ = BC = 2$,$CQ = BF = 22$。由对称,得$BF = B'F = 22$,
∴ $B'Q = B'F - QF = 20$。在$Rt\triangle B'CQ$中,由勾股定理,得$B'C^{2}=\sqrt{CQ^{2}+B'Q^{2}}=2\sqrt{221}$,即$CH + HB$的最小值为$2\sqrt{221}$。
∴ $2OM + HB$的最小值为$2\sqrt{221}$。

查看更多完整答案,请扫码查看


