22. (10分)(河北中考)我国的探月工程激发了同学们对太空的兴趣. 如图,淇淇在家透过窗户的最高点P恰好看到一颗星星,此时淇淇距窗户的水平距离BQ = 4 m,仰角为α;淇淇向前走了3 m后到达点D,透过点P恰好看到月亮,仰角为β. 已知淇淇的眼睛与水平地面BQ的距离AB = CD = 1.6 m,点P到BQ的距离PQ = 2.6 m,AC的延长线交PQ于点E(注:图中所有点均在同一平面). 求:
(1) 仰角β的度数及tan α的值;
(2) CP的长及sin ∠APC的值.

(1) 仰角β的度数及tan α的值;
(2) CP的长及sin ∠APC的值.

答案:
(1) 由题意,得$PQ\perp AE,PQ = 2.6\ m,AB = CD = EQ = 1.6\ m,AE = BQ = 4\ m,AC = BD = 3\ m,\therefore CE = 4 - 3 = 1(m),PE = 2.6 - 1.6 = 1(m),\angle CEP = 90^{\circ}$. $\therefore CE = PE$. $\therefore\beta=\angle PCE=\angle CPE=\frac{180^{\circ}-\angle CEP}{2}=45^{\circ},\tan\alpha=\tan\angle PAE=\frac{PE}{AE}=\frac{1}{4}$
(2) $\because CE = PE = 1\ m,\angle CEP = 90^{\circ},\therefore$由勾股定理,得$CP=\sqrt{1^{2}+1^{2}}=\sqrt{2}(m)$. 如图,过点$C$作$CH\perp AP$于点$H$. $\because\tan\alpha=\tan\angle PAE=\frac{CH}{AH}=\frac{1}{4},\therefore$设$CH = x\ m$,则$AH = 4x\ m$. $\therefore$在$Rt\triangle ACH$中,由勾股定理,得$x^{2}+(4x)^{2}=9$,解得$x=\frac{3\sqrt{17}}{17}$(负值舍去). $\therefore CH=\frac{3\sqrt{17}}{17}\ m$. $\therefore\sin\angle APC=\frac{CH}{CP}=\frac{\frac{3\sqrt{17}}{17}}{\sqrt{2}}=\frac{3\sqrt{34}}{34}$

(1) 由题意,得$PQ\perp AE,PQ = 2.6\ m,AB = CD = EQ = 1.6\ m,AE = BQ = 4\ m,AC = BD = 3\ m,\therefore CE = 4 - 3 = 1(m),PE = 2.6 - 1.6 = 1(m),\angle CEP = 90^{\circ}$. $\therefore CE = PE$. $\therefore\beta=\angle PCE=\angle CPE=\frac{180^{\circ}-\angle CEP}{2}=45^{\circ},\tan\alpha=\tan\angle PAE=\frac{PE}{AE}=\frac{1}{4}$
(2) $\because CE = PE = 1\ m,\angle CEP = 90^{\circ},\therefore$由勾股定理,得$CP=\sqrt{1^{2}+1^{2}}=\sqrt{2}(m)$. 如图,过点$C$作$CH\perp AP$于点$H$. $\because\tan\alpha=\tan\angle PAE=\frac{CH}{AH}=\frac{1}{4},\therefore$设$CH = x\ m$,则$AH = 4x\ m$. $\therefore$在$Rt\triangle ACH$中,由勾股定理,得$x^{2}+(4x)^{2}=9$,解得$x=\frac{3\sqrt{17}}{17}$(负值舍去). $\therefore CH=\frac{3\sqrt{17}}{17}\ m$. $\therefore\sin\angle APC=\frac{CH}{CP}=\frac{\frac{3\sqrt{17}}{17}}{\sqrt{2}}=\frac{3\sqrt{34}}{34}$

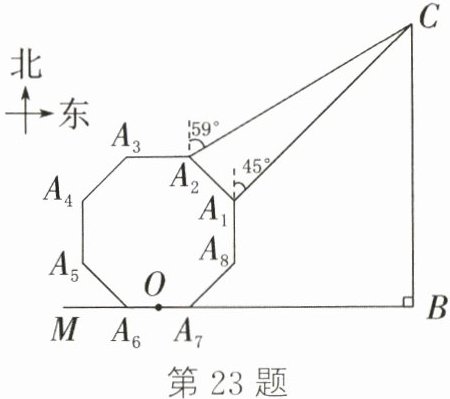
23. (12分)(连云港中考)数学兴趣小组进行了如下探究:如图,正八边形游乐城A₁A₂A₃A₄A₅A₆A₇A₈的边长为$\frac{\sqrt{2}}{2}$ km,南门O设立在边A₆A₇的正中央,游乐城南侧有一条东西走向的道路BM,A₆A₇在BM上(门宽及门与道路间的距离忽略不计),东侧有一条南北走向的道路BC,C处有一座雕塑. 在A₁处测得雕塑在北偏东45°方向上,在A₂处测得雕塑在北偏东59°方向上(参考数据:sin 76°≈1.0,tan 76°≈4.0,sin 59°≈0.9,tan 59°≈1.7).
(1) ∠CA₁A₂ = ________°,∠CA₂A₁ = ________°;
(2) 求A₁处到道路BC的距离;
(3) 若该小组成员小李出南门O后沿道路MB向东行走,则他离B处不超过多少千米,才能确保观察雕塑不会受到游乐城的影响?
(1) ∠CA₁A₂ = ________°,∠CA₂A₁ = ________°;
(2) 求A₁处到道路BC的距离;
(3) 若该小组成员小李出南门O后沿道路MB向东行走,则他离B处不超过多少千米,才能确保观察雕塑不会受到游乐城的影响?

答案:
(1) 90 76 解析: $\because$八边形$A_{1}A_{2}A_{3}A_{4}A_{5}A_{6}A_{7}A_{8}$是正八边形,$\therefore$外角$=\frac{360^{\circ}}{8}=45^{\circ}$. $\therefore\angle CA_{1}A_{2}=45^{\circ}+45^{\circ}=90^{\circ},\angle CA_{2}A_{1}=45^{\circ}+(90^{\circ}-59^{\circ})=76^{\circ}$.
(2) 如图, 过点$A_{1}$作$A_{1}D\perp BC$于点$D$. 在$Rt\triangle CA_{2}A_{1}$中,$A_{2}A_{1}=\frac{\sqrt{2}}{2}\ km,\angle CA_{2}A_{1}=76^{\circ},\therefore CA_{1}=A_{1}A_{2}\cdot\tan76^{\circ}\approx\frac{\sqrt{2}}{2}\times4.0 = 2\sqrt{2}(km)$. 在$Rt\triangle CA_{1}D$中,易知$\angle CA_{1}D = 45^{\circ},\therefore A_{1}D = CA_{1}\cdot\cos45^{\circ}=2\sqrt{2}\times\frac{\sqrt{2}}{2}=2(km)$,即$A_{1}$处到道路$BC$的距离约为$2\ km$
(3) 如图,连接$CA_{8}$并延长交$BM$于点$E$,延长$A_{1}A_{8}$交$BE$于点$G$,过点$A_{8}$作$A_{8}F\perp BC$于点$F$. $\because$正八边形的外角均为$45^{\circ},\therefore\angle A_{7}A_{8}G=\angle A_{8}A_{7}G = 45^{\circ}$. $\therefore\angle A_{8}GA_{7}=180^{\circ}-45^{\circ}-45^{\circ}=90^{\circ}$. $\therefore$在$Rt\triangle A_{7}A_{8}G$中,$A_{8}G = A_{7}A_{8}\cdot\sin45^{\circ}=\frac{\sqrt{2}}{2}\times\frac{\sqrt{2}}{2}=\frac{1}{2}(km)$. 易得$FB = A_{8}G=\frac{1}{2}\ km,A_{8}F = A_{1}D = 2\ km,DF = A_{1}A_{8}=\frac{\sqrt{2}}{2}\ km$. $\because$在$Rt\triangle CA_{1}D$中,$CD = CA_{1}\cdot\sin45^{\circ}=2\ km,\therefore CF = CD + DF=(2+\frac{\sqrt{2}}{2})\ km,CB = CD + DF + FB=\frac{5+\sqrt{2}}{2}\ km$. $\because A_{8}F\perp BC,CB\perp BM,\therefore\angle CFA_{8}=\angle B = 90^{\circ}$. 又$\because\angle FCA_{8}=\angle BCE,\therefore\triangle CA_{8}F\sim\triangle CEB$. $\therefore\frac{CF}{CB}=\frac{A_{8}F}{EB}$. $\therefore\frac{2+\frac{\sqrt{2}}{2}}{\frac{5+\sqrt{2}}{2}}=\frac{2}{EB}$. $\therefore EB=\frac{18 - \sqrt{2}}{7}\ km$. $\therefore$小李离点$B$不超过$\frac{18 - \sqrt{2}}{7}\ km$,才能确保观察雕塑不会受到游乐城的影响

(1) 90 76 解析: $\because$八边形$A_{1}A_{2}A_{3}A_{4}A_{5}A_{6}A_{7}A_{8}$是正八边形,$\therefore$外角$=\frac{360^{\circ}}{8}=45^{\circ}$. $\therefore\angle CA_{1}A_{2}=45^{\circ}+45^{\circ}=90^{\circ},\angle CA_{2}A_{1}=45^{\circ}+(90^{\circ}-59^{\circ})=76^{\circ}$.
(2) 如图, 过点$A_{1}$作$A_{1}D\perp BC$于点$D$. 在$Rt\triangle CA_{2}A_{1}$中,$A_{2}A_{1}=\frac{\sqrt{2}}{2}\ km,\angle CA_{2}A_{1}=76^{\circ},\therefore CA_{1}=A_{1}A_{2}\cdot\tan76^{\circ}\approx\frac{\sqrt{2}}{2}\times4.0 = 2\sqrt{2}(km)$. 在$Rt\triangle CA_{1}D$中,易知$\angle CA_{1}D = 45^{\circ},\therefore A_{1}D = CA_{1}\cdot\cos45^{\circ}=2\sqrt{2}\times\frac{\sqrt{2}}{2}=2(km)$,即$A_{1}$处到道路$BC$的距离约为$2\ km$
(3) 如图,连接$CA_{8}$并延长交$BM$于点$E$,延长$A_{1}A_{8}$交$BE$于点$G$,过点$A_{8}$作$A_{8}F\perp BC$于点$F$. $\because$正八边形的外角均为$45^{\circ},\therefore\angle A_{7}A_{8}G=\angle A_{8}A_{7}G = 45^{\circ}$. $\therefore\angle A_{8}GA_{7}=180^{\circ}-45^{\circ}-45^{\circ}=90^{\circ}$. $\therefore$在$Rt\triangle A_{7}A_{8}G$中,$A_{8}G = A_{7}A_{8}\cdot\sin45^{\circ}=\frac{\sqrt{2}}{2}\times\frac{\sqrt{2}}{2}=\frac{1}{2}(km)$. 易得$FB = A_{8}G=\frac{1}{2}\ km,A_{8}F = A_{1}D = 2\ km,DF = A_{1}A_{8}=\frac{\sqrt{2}}{2}\ km$. $\because$在$Rt\triangle CA_{1}D$中,$CD = CA_{1}\cdot\sin45^{\circ}=2\ km,\therefore CF = CD + DF=(2+\frac{\sqrt{2}}{2})\ km,CB = CD + DF + FB=\frac{5+\sqrt{2}}{2}\ km$. $\because A_{8}F\perp BC,CB\perp BM,\therefore\angle CFA_{8}=\angle B = 90^{\circ}$. 又$\because\angle FCA_{8}=\angle BCE,\therefore\triangle CA_{8}F\sim\triangle CEB$. $\therefore\frac{CF}{CB}=\frac{A_{8}F}{EB}$. $\therefore\frac{2+\frac{\sqrt{2}}{2}}{\frac{5+\sqrt{2}}{2}}=\frac{2}{EB}$. $\therefore EB=\frac{18 - \sqrt{2}}{7}\ km$. $\therefore$小李离点$B$不超过$\frac{18 - \sqrt{2}}{7}\ km$,才能确保观察雕塑不会受到游乐城的影响

查看更多完整答案,请扫码查看


