17. 如图,礼盒的上、下底面为全等的正六边形,其主视图与左视图均由矩形构成,主视图中大矩形的长与宽如图所示,左视图中两个小矩形全等. 如果用彩色胶带按如图所示的方式包扎礼盒,那么所需胶带长度至少为_______cm.
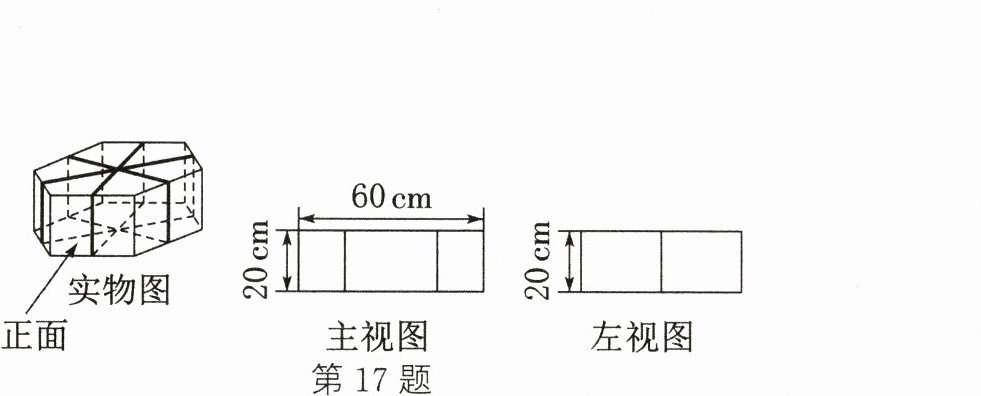

答案:
$(180\sqrt{3}+120)$
18. 如图所示为一个几何体的三视图(单位:cm),则这个几何体侧面展开图的圆心角度数是_______.
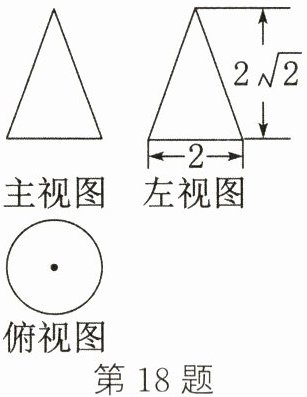

答案:
$120^{\circ}$
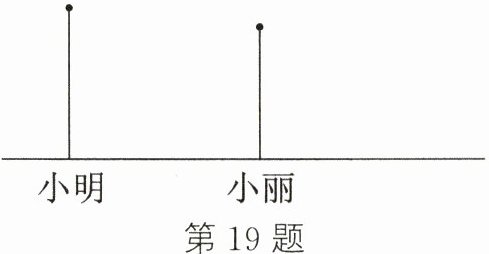
19.(5分)小明和小丽在操场上玩耍,小丽突然高兴地对小明说:“我踩到你的‘脑袋’了.”如图所示为此时小明和小丽的位置.
(1)请画出此时小丽在阳光下的影子;
(2)若已知小明身高为1.6 m,小明和小丽之间的距离为2 m,而小丽的影子长为1.75 m,求小丽的身高.
(1)请画出此时小丽在阳光下的影子;
(2)若已知小明身高为1.6 m,小明和小丽之间的距离为2 m,而小丽的影子长为1.75 m,求小丽的身高.

答案:
(1)如图所示 (2)设小丽的身高为 $x$ m. $\because$ 小明身高为 1.6 m,小明和小丽之间的距离为 2 m,而小丽的影子长为 1.75 m,
$\therefore\frac{x}{1.6}=\frac{1.75}{2}$,解得 $x = 1.4$. $\therefore$ 小丽的身高为 1.4 m

(1)如图所示 (2)设小丽的身高为 $x$ m. $\because$ 小明身高为 1.6 m,小明和小丽之间的距离为 2 m,而小丽的影子长为 1.75 m,
$\therefore\frac{x}{1.6}=\frac{1.75}{2}$,解得 $x = 1.4$. $\therefore$ 小丽的身高为 1.4 m

20.(6分)如图所示为一个正六棱柱,画出它的三视图.
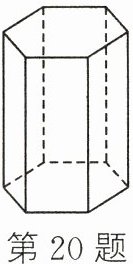

答案:
如图所示
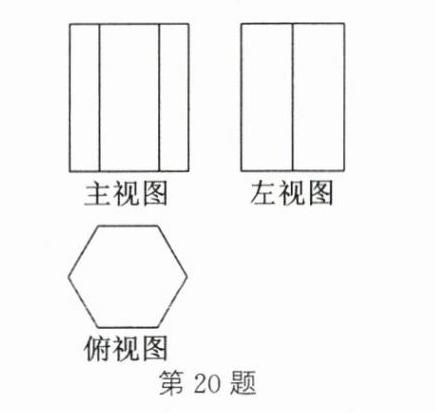
如图所示

21.(8分)如图,AB是公园的一圆形桌面的主视图(桌面厚度忽略不计),MN表示该桌面在路灯下的影子,CD表示一圆形凳面的主视图(凳面厚度忽略不计).
(1)请标出路灯O的位置,并画出CD的影子PQ;
(2)若桌面直径和桌面与地面之间的距离均为1.2 m,测得MN = 2 m,求路灯O到地面的距离.

(1)请标出路灯O的位置,并画出CD的影子PQ;
(2)若桌面直径和桌面与地面之间的距离均为1.2 m,测得MN = 2 m,求路灯O到地面的距离.

答案:
(1)如图所示 (2)如图,过点 $O$ 作 $OF\perp MQ$ 于点 $F$,交 $AB$ 的延长线于点 $E$. 由题意,得 $AE\perp OF$,$AB = 1.2$ m,$EF = 1.2$ m,$MN = 2$ m. $\because AB// MN$,$\therefore\triangle OAB\sim\triangle OMN$,$\triangle OAE\sim\triangle OMF$.
$\therefore\frac{AB}{MN}=\frac{OB}{ON}$,$\frac{OE}{OF}=\frac{OB}{ON}$. $\therefore\frac{AB}{MN}=\frac{OE}{OF}$. $\therefore\frac{1.2}{2}=\frac{OF - 1.2}{OF}$.
$\therefore OF = 3$ m. $\therefore$ 路灯 $O$ 到地面的距离为 3 m

(1)如图所示 (2)如图,过点 $O$ 作 $OF\perp MQ$ 于点 $F$,交 $AB$ 的延长线于点 $E$. 由题意,得 $AE\perp OF$,$AB = 1.2$ m,$EF = 1.2$ m,$MN = 2$ m. $\because AB// MN$,$\therefore\triangle OAB\sim\triangle OMN$,$\triangle OAE\sim\triangle OMF$.
$\therefore\frac{AB}{MN}=\frac{OB}{ON}$,$\frac{OE}{OF}=\frac{OB}{ON}$. $\therefore\frac{AB}{MN}=\frac{OE}{OF}$. $\therefore\frac{1.2}{2}=\frac{OF - 1.2}{OF}$.
$\therefore OF = 3$ m. $\therefore$ 路灯 $O$ 到地面的距离为 3 m

查看更多完整答案,请扫码查看


