《2024年同步练习册海燕出版社六年级数学上册人教版》

1. 根据下面前三个算式的规律,填一填。
$1+2+1= 4= 2^{2}$ $1+2+3+2+1= 9= 3^{2}$ $1+2+3+4+3+2+1= 16= 4^{2}$
$1+2+3+4+5+4+3+2+1= ( )= ( )^{2}$
$1+2+3+4+5+6+7+8+9+8+7+6+5+4+3+2+1= ( )= ( )^{2}$

答案： 25
5
81
9

2. 下面各图形中有几个点？按规律画出下一个图形。

$1+2= 3$ $1+2+4= ( )$ $1+2+4+6= ( )$ ( )

答案：

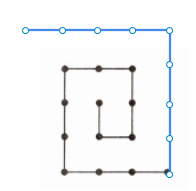
7
13
1+2+4+6+8=21

3. 某餐厅摆放桌椅如下。

1 张餐桌可坐 8 人,2 张餐桌可坐 14 人,5 张餐桌可坐( )人。按此规律,$n(n≥2)$张餐桌可坐( )人。
1 条直线可以把一个平面分成 2 个区域(如下图①),2 条直线最多可以把一个平面分成 4 个区域(如下图②)。5 条直线最多可以把一个平面分成几个区域？10 条呢？

答案：

32
2+6n
1条直线，2个区域，1+1=2； .
2条直线，4个区域，1+1+2=4；
3条直线，7个区域，1+1+2+3=7；
4条直线，11个区域，1+1+2+3+4=11；
5条直线，1+1+2+3+4+5=16(个)
10条直线，1+1+2+3…+10=56(个)
答： 5条直线最多可以把一个平面分成16个区域。10条最多可以把一个平面分成56个区域。