《2024年同步练习册海燕出版社六年级数学上册人教版》

1. 下面图形中哪些角是圆心角？在括号里画“√”。
- 第一个图：未标记圆心,以 $AB$ 为边的角( )

- 第二个图：圆心为 $O$,以 $OA$、$OB$ 为边的角(√ )
- 第三个图：圆心为 $O$,以 $OA$、$OB$ 为边的角,但角的开口方向与第二图不同(√ )
- 第四个图：圆心为 $O$,$A$、$B$ 在圆上,但角的顶点为 $A$( )

答案：
√
√

2. 判断。(对的在括号里画“√”,错的画“×”。)
(1) 圆是扇形的一部分。( × )
(2) 在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关。( √ )

答案： ×
√

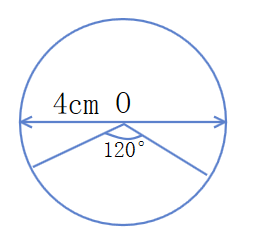
3. 画一个直径是 $4cm$ 的圆,再在圆中画一个圆心角是 $120°$ 的扇形。

答案：

4. 计算下面扇形和扇环的面积。
- 扇形：半径 $5cm$,圆心角 $90°$ 的扇形。

- 扇环：外圆半径 $8dm$,内圆半径 $4dm$,圆心角 $90°$ 的扇环。

计算下面扇环的面积。
外圆半径 $6m$,内圆半径 $3m$,圆心角 $60°$ 的扇环。

答案： $​ \frac {90°}{360°}×5^2×3.14=19.625(\mathrm {cm}^2)​$
$​ \frac {90°}{360°}×8^2×3.14-\frac {90°}{360°}×4^2×3.14=37.68 (\mathrm {dm}^2)​$
$​ \frac {60°}{360°}×6^2×3.14-\frac {60°}{360°}×3^2×3.14=14.13 (\mathrm {m^2})​$
答：扇环的面积为​14.13​平方米。