第67页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
1. 填一填。
(1) 用圆规画一个周长是 $31.4cm$ 的圆,圆规两脚间的距离是( )$cm$。
(2) 右图有( )条对称轴。

(3) 两个同心圆,内圆半径是 $4cm$,外圆半径是 $6cm$,圆环的面积是( )。
(4) 一个圆的周长是 $62.8cm$,这个圆内最大的正方形的面积是( )。
(5) 以半圆为弧的扇形的圆心角是( )$^{\circ}$。
(1) 用圆规画一个周长是 $31.4cm$ 的圆,圆规两脚间的距离是( )$cm$。
(2) 右图有( )条对称轴。

(3) 两个同心圆,内圆半径是 $4cm$,外圆半径是 $6cm$,圆环的面积是( )。
(4) 一个圆的周长是 $62.8cm$,这个圆内最大的正方形的面积是( )。
(5) 以半圆为弧的扇形的圆心角是( )$^{\circ}$。
答案:
5
4
62.8cm²
200cm²
180
4
62.8cm²
200cm²
180
2. 看图计算。
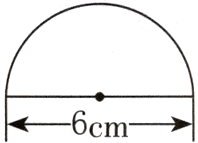
(1) 求下面半圆的周长。
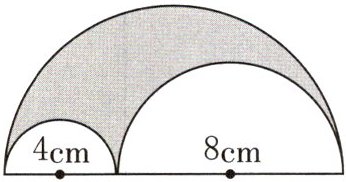
(2) 求下面图形中涂色部分的面积。
(1) 求下面半圆的周长。


(2) 求下面图形中涂色部分的面积。
答案:
$6+\frac 12×6×3.14=15.42 (\mathrm {cm})$
$\frac 12×[(4+8)÷2]^2×3.14-\frac 12×(4÷2)^2×3.14-$
$\frac 12×(8÷2)^2×3.14=25.12(\mathrm {cm}^2)$
$\frac 12×[(4+8)÷2]^2×3.14-\frac 12×(4÷2)^2×3.14-$
$\frac 12×(8÷2)^2×3.14=25.12(\mathrm {cm}^2)$
3. 李老师的自行车轮胎的外直径约为 $5dm$,他家到学校的距离是 $1.727km$。李老师骑行时,自行车的轮胎平均每分钟转 $110$ 圈,他从学校骑行到家约需多长时间?
答案:
1.727km=17270dm
17270÷(5×3.14)÷110=10 (分钟)
答:他从学校骑行到家约需10分钟。
17270÷(5×3.14)÷110=10 (分钟)
答:他从学校骑行到家约需10分钟。
4. 右图中圆的周长是 $25.12cm$,圆的面积正好等于长方形 $OABC$ 面积的 $2$ 倍。求涂色部分的面积。
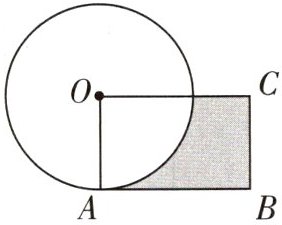

答案:
$ 25.12÷3.14÷2=4(\mathrm {cm})$
$4^2×3.14÷2-\frac 14×4^2×3.14=12.56(\mathrm {cm}^2)$
答:涂色部分的面积为12.56平方厘米。
位置
大小
2
周长
面积
圆周长的一半
半径
长
宽
πr
r
πr²
S=πr²
$ \frac π4$
$ \frac 2π$
圆心角的大小
$4^2×3.14÷2-\frac 14×4^2×3.14=12.56(\mathrm {cm}^2)$
答:涂色部分的面积为12.56平方厘米。
位置
大小
2
周长
面积
圆周长的一半
半径
长
宽
πr
r
πr²
S=πr²
$ \frac π4$
$ \frac 2π$
圆心角的大小
5. 圆的知识梳理
| 知识点 | 详细内容 |
| 圆的认识 | 圆心决定圆的( ),半径决定圆的( )。在同一个圆中,所有的半径都相等,所有的直径都相等。在同一个圆或等圆中,$d = 2r$,$r= \frac{d}{2}$。 |
| 圆的画法 | 先根据半径确定圆规两脚间的距离,然后把圆规有针尖的脚固定在一点上,最后将装有铅笔(铅笔芯)的脚旋转一周。 |
| 圆的周长 | 围成圆的曲线的长是圆的周长。圆的周长 $=$ 直径 $×$ 圆周率 $C = \pi d$ 圆的周长 $=$ 半径 $×$( )$×$ 圆周率 $C = 2\pi r$ |
| 圆的面积 | 如上图,把圆剪拼成一个近似的长方形,( )变了,( )没变。从图中可以看出,长方形的长近似于( ),宽近似于( ),因为长方形的面积 $=$( )$×$( ),所以圆的面积 $=$( )$×$( )$=$( )。因此圆的面积计算公式是( )。在一个正方形内画一个最大的圆,圆的面积是正方形面积的( )。在一个圆内画一个最大的正方形,正方形的面积是圆面积的( )。 |
| 圆环的面积 | $S= \pi R^{2}-\pi r^{2}= \pi(R^{2}-r^{2})$ |
| 扇形 | 圆心角具备的两个条件:①顶点是圆心;②角的两条边是圆的半径。在同一个圆中,扇形的大小与这个扇形的( )有关。 |
| 知识点 | 详细内容 |
| 圆的认识 | 圆心决定圆的( ),半径决定圆的( )。在同一个圆中,所有的半径都相等,所有的直径都相等。在同一个圆或等圆中,$d = 2r$,$r= \frac{d}{2}$。 |
| 圆的画法 | 先根据半径确定圆规两脚间的距离,然后把圆规有针尖的脚固定在一点上,最后将装有铅笔(铅笔芯)的脚旋转一周。 |
| 圆的周长 | 围成圆的曲线的长是圆的周长。圆的周长 $=$ 直径 $×$ 圆周率 $C = \pi d$ 圆的周长 $=$ 半径 $×$( )$×$ 圆周率 $C = 2\pi r$ |
| 圆的面积 | 如上图,把圆剪拼成一个近似的长方形,( )变了,( )没变。从图中可以看出,长方形的长近似于( ),宽近似于( ),因为长方形的面积 $=$( )$×$( ),所以圆的面积 $=$( )$×$( )$=$( )。因此圆的面积计算公式是( )。在一个正方形内画一个最大的圆,圆的面积是正方形面积的( )。在一个圆内画一个最大的正方形,正方形的面积是圆面积的( )。 |
| 圆环的面积 | $S= \pi R^{2}-\pi r^{2}= \pi(R^{2}-r^{2})$ |
| 扇形 | 圆心角具备的两个条件:①顶点是圆心;②角的两条边是圆的半径。在同一个圆中,扇形的大小与这个扇形的( )有关。 |
答案:
查看更多完整答案,请扫码查看


