《2025年全优标准卷八年级数学上册人教版》

22. (10 分)材料 1:教科书中这样写道:“我们把多项式$a^{2}+2ab+b^{2}$及$a^{2}-2ab+b^{2}$叫作完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫作配方法. 例如:分解因式:$x^{2}+2x-3=(x^{2}+2x+1)-4=(x+1)^{2}-4=(x+1+2)(x+1-2)=(x+3)(x-1)$.
材料 2:分解因式$(a+b)^{2}+2(a+b)+1$.
解:设$a+b=x$,则原式$=x^{2}+2x+1=(x+1)^{2}=(a+b+1)^{2}$.
这样的解题方法叫作“换元法”,即当复杂的多项式中,某部分重复出现时,我们用字母将其替换,从而简化这个多项式. 换元法是一个重要的数学方法,不少问题能用换元法解决.
请你根据以上阅读材料解答下列问题:
(1)根据材料 1 将$x^{2}+4x+3$因式分解;
(2)根据材料 2 将$(x-y)^{2}-10(x-y)+25$因式分解;
(3)结合材料 1 和材料 2,将$(m^{2}-2m)(m^{2}-2m-3)-4$因式分解.

答案： 22.解：
(1)原式$=x^{2}+4x+4-1=(x+2)^{2}-1=(x+$
2+1)(x+2-1)=(x+3)(x+1).
(2)设x-y=a，则原式$=a^{2}-10a+25=(a-5)^{2}=$
$(x-y-5)^{2}.$
(3)设$m^{2}-2m=a，$则原式$=a(a-3)-4=a^{2}-3a-$
$4=a^{2}-3a+\frac{9}{4}-\frac{25}{4}=(a-\frac{3}{2})^{2}-\frac{25}{4}=(a-\frac{3}{2}+$
$\frac{5}{2})(a-\frac{3}{2}-\frac{5}{2})=(a+1)(a-4)=(m^{2}-2m+1)(m^{2}-2m-4)=(m-1)^{2}(m^{2}-2m-4).$

$23. (11 $分$)$数学活动课上$,$老师准备了若干张如图$ 1 $所示的三种纸片$,A $种纸片是边长为$a$的正方形$,B $种纸片是边长为$b$的正方形$,C $种纸片是长为$b,$宽为$a$的长方形$,$并用一张$ A $种纸片$,$一张$ B $种纸片$,$两张$ C $种纸片拼成如图$ 2 $所示的大正方形$.$　　

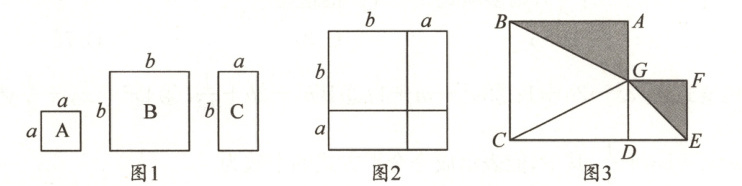
$(1)$观察图$ 2,$请你写出代数式$(a+b)^{2},a^{2}+b^{2},ab$之间的等量关系$:$　　$(a+b)^{2}=a^{2}+b^{2}+2ab$　　$;$　　
$(2)$根据$(2)$中的等量关系$,$解决问题$:$已知$a+b=5,a^{2}+b^{2}=11,$求$ab$的值$;$　　
$(3)$如图$,$在线段$CE$上取一点$D,$分别以$CD,DE$为边作正方形$ABCD$和正方形$DEFG,$连接$BG,CG,EG. $若阴影部分的面积和为$ 30,\triangle CDG$的面积为$ 14,$求$CE$的长度$.$　　

答案： 23.解：$(1)(a+b)^{2}=a^{2}+b^{2}+2ab 【$解析$】\because$从“整
体”上看，大正方形的边长为a+b，因此面积为
$(a+b)^{2}，$而拼成图2的四个部分的面积和为$a^{2}+$
$b^{2}+2ab,\therefore(a+b)^{2}=a^{2}+b^{2}+2ab.$
(2)由
(1)得$a^{2}+b^{2}=(a+b)^{2}-2ab.$
$\because a+b=5,a^{2}+b^{2}=11，$
$\therefore11=5^{2}-2ab，$解得ab=7.
(3)设正方形ABCD的边长为p，正方形DEFG
的边长为q.
$\because$阴影部分的面积和为30，$\triangle CDG$的面积为14，
$\therefore\frac{1}{2}p(p-q)+\frac{1}{2}q^{2}=30,\frac{1}{2}pq=14，$
$\therefore p^{2}+q^{2}=88,pq=28.$
$\because(p+q)^{2}=p^{2}+q^{2}+2pq=88+2×28=144，$
$\therefore p+q=12($负值已舍去)，即CE的长度为12.