搜索
2025年全优标准卷八年级数学上册人教版
注：目前有些书本章节名称可能整理的还不是很完善，但都是按照顺序排列的，请同学们按照顺序仔细查找。练习册 2025年全优标准卷八年级数学上册人教版 答案主要是用来给同学们做完题方便对答案用的，请勿直接抄袭。
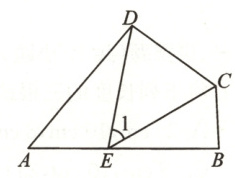
22. (8 分)如图,在四边形 ABCD 中,∠B+∠ADC=180°,CE 平分∠BCD 交 AB 于点 E,连接 DE.
(1)若∠A=50°,∠B=85°,求∠BEC 的度数;
(2)若∠CDE=∠DCE,求证:∠A=∠1.
(1)若∠A=50°,∠B=85°,求∠BEC 的度数;
(2)若∠CDE=∠DCE,求证:∠A=∠1.
答案：
22.
(1)解:$\because \angle B + \angle ADC = 180^{\circ}$，$\angle A + \angle B + \angle BCD + \angle ADC = 360^{\circ}$，$\therefore \angle A + \angle BCD = 180^{\circ}$。$\because \angle A = 50^{\circ}$，$\therefore \angle BCD = 130^{\circ}$。$\because CE$平分$\angle BCD$，$\therefore \angle BCE = \frac{1}{2}\angle BCD = 65^{\circ}$。又$\angle B = 85^{\circ}$，$\therefore \angle BEC = 180^{\circ} - \angle BCE - \angle B = 180^{\circ} - 65^{\circ} - 85^{\circ} = 30^{\circ}$。
(2)证明:由
(1)知$\angle A + \angle BCD = 180^{\circ}$，$\therefore \angle A + \angle BCE + \angle DCE = 180^{\circ}$。$\because CE$平分$\angle BCD$，$\therefore \angle DCE = \angle BCE$，$\therefore \angle A + 2\angle DCE = 180^{\circ}$。$\because \angle CDE = \angle DCE$，$\therefore \angle1 + \angle CDE + \angle DCE = \angle1 + 2\angle DCE = 180^{\circ}$。$\therefore \angle A = \angle1$。
(1)解:$\because \angle B + \angle ADC = 180^{\circ}$，$\angle A + \angle B + \angle BCD + \angle ADC = 360^{\circ}$，$\therefore \angle A + \angle BCD = 180^{\circ}$。$\because \angle A = 50^{\circ}$，$\therefore \angle BCD = 130^{\circ}$。$\because CE$平分$\angle BCD$，$\therefore \angle BCE = \frac{1}{2}\angle BCD = 65^{\circ}$。又$\angle B = 85^{\circ}$，$\therefore \angle BEC = 180^{\circ} - \angle BCE - \angle B = 180^{\circ} - 65^{\circ} - 85^{\circ} = 30^{\circ}$。
(2)证明:由
(1)知$\angle A + \angle BCD = 180^{\circ}$，$\therefore \angle A + \angle BCE + \angle DCE = 180^{\circ}$。$\because CE$平分$\angle BCD$，$\therefore \angle DCE = \angle BCE$，$\therefore \angle A + 2\angle DCE = 180^{\circ}$。$\because \angle CDE = \angle DCE$，$\therefore \angle1 + \angle CDE + \angle DCE = \angle1 + 2\angle DCE = 180^{\circ}$。$\therefore \angle A = \angle1$。
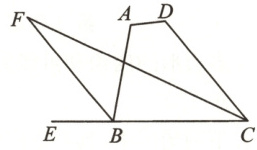
23. (10 分)如图,四边形 ABCD 的内角∠BCD 的平分线与外角∠ABE 的平分线相交于点 F.
(1)若 BF//CD,∠ABC=80°,求∠BCD 的度数;
(2)若∠A=110°,∠D=120°,求∠F 的度数;
(3)猜想∠F,∠A,∠D 之间的数量关系,并说明理由.
(1)若 BF//CD,∠ABC=80°,求∠BCD 的度数;
(2)若∠A=110°,∠D=120°,求∠F 的度数;
(3)猜想∠F,∠A,∠D 之间的数量关系,并说明理由.
答案：
23.
(1)解:$\because \angle ABC = 80^{\circ}$，$\therefore \angle ABE = 180^{\circ} - 80^{\circ} = 100^{\circ}$。$\because BF$平分$\angle ABE$，$\therefore \angle ABF = \angle EBF = 50^{\circ}$。$\because BF// CD$，$\therefore \angle BCD = \angle EBF = 50^{\circ}$。
(2)解:$\because CF$平分$\angle BCD$，$BF$平分$\angle ABE$，$\therefore \angle BCF = \angle DCF = \frac{1}{2}\angle BCD$，$\angle EBF = \angle ABF = \frac{1}{2}\angle ABE$。$\because \angle A + \angle D + \angle ABC + \angle BCD = 360^{\circ}$，$\angle A = 110^{\circ}$，$\angle D = 120^{\circ}$，$\therefore \angle ABC + \angle BCD = 360^{\circ} - 110^{\circ} - 120^{\circ} = 130^{\circ}$，即$180^{\circ} - \angle ABE + 2\angle BCF = 130^{\circ}$。$\because \angle ABE = 2\angle EBF$，$\angle EBF = \angle F + \angle BCF$，$\therefore 180^{\circ} - 2(\angle F + \angle BCF) + 2\angle BCF = 130^{\circ}$，$\therefore 2\angle F = 50^{\circ}$，$\therefore \angle F = 25^{\circ}$。
(3)$\angle F = \frac{1}{2}(\angle A + \angle D - 180^{\circ})$，理由如下：$\because \angle A + \angle D + \angle ABC + \angle BCD = 360^{\circ}$，$\angle ABC = 180^{\circ} - \angle ABE$，$\angle ABE = 2\angle EBF$，$\angle BCD = 2\angle BCF$，$\angle EBF = \angle F + \angle BCF$，$\therefore \angle A + \angle D + 180^{\circ} - \angle ABE + 2\angle BCF = 360^{\circ}$，即$\angle A + \angle D - 2\angle EBF + 2\angle BCF = 180^{\circ}$，即$\angle A + \angle D - 2(\angle F + \angle BCF) + 2\angle BCF = 180^{\circ}$，即$2\angle F = \angle A + \angle D - 180^{\circ}$，$\therefore \angle F = \frac{1}{2}(\angle A + \angle D - 180^{\circ})$。
(1)解:$\because \angle ABC = 80^{\circ}$，$\therefore \angle ABE = 180^{\circ} - 80^{\circ} = 100^{\circ}$。$\because BF$平分$\angle ABE$，$\therefore \angle ABF = \angle EBF = 50^{\circ}$。$\because BF// CD$，$\therefore \angle BCD = \angle EBF = 50^{\circ}$。
(2)解:$\because CF$平分$\angle BCD$，$BF$平分$\angle ABE$，$\therefore \angle BCF = \angle DCF = \frac{1}{2}\angle BCD$，$\angle EBF = \angle ABF = \frac{1}{2}\angle ABE$。$\because \angle A + \angle D + \angle ABC + \angle BCD = 360^{\circ}$，$\angle A = 110^{\circ}$，$\angle D = 120^{\circ}$，$\therefore \angle ABC + \angle BCD = 360^{\circ} - 110^{\circ} - 120^{\circ} = 130^{\circ}$，即$180^{\circ} - \angle ABE + 2\angle BCF = 130^{\circ}$。$\because \angle ABE = 2\angle EBF$，$\angle EBF = \angle F + \angle BCF$，$\therefore 180^{\circ} - 2(\angle F + \angle BCF) + 2\angle BCF = 130^{\circ}$，$\therefore 2\angle F = 50^{\circ}$，$\therefore \angle F = 25^{\circ}$。
(3)$\angle F = \frac{1}{2}(\angle A + \angle D - 180^{\circ})$，理由如下：$\because \angle A + \angle D + \angle ABC + \angle BCD = 360^{\circ}$，$\angle ABC = 180^{\circ} - \angle ABE$，$\angle ABE = 2\angle EBF$，$\angle BCD = 2\angle BCF$，$\angle EBF = \angle F + \angle BCF$，$\therefore \angle A + \angle D + 180^{\circ} - \angle ABE + 2\angle BCF = 360^{\circ}$，即$\angle A + \angle D - 2\angle EBF + 2\angle BCF = 180^{\circ}$，即$\angle A + \angle D - 2(\angle F + \angle BCF) + 2\angle BCF = 180^{\circ}$，即$2\angle F = \angle A + \angle D - 180^{\circ}$，$\therefore \angle F = \frac{1}{2}(\angle A + \angle D - 180^{\circ})$。
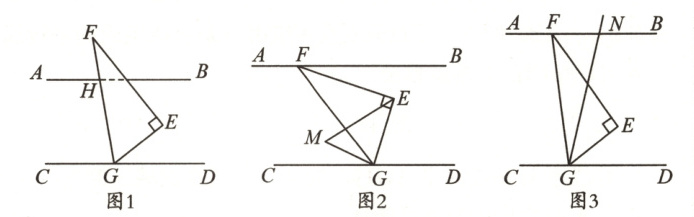
24. (13 分)在综合与实践课上,老师让同学们以“三角尺与平行线”为主题开展数学活动. 已知直线 AB,CD,直角三角尺 EFG,AB//CD,∠FEG=90°,∠EGF=60°.
(1)小明将三角尺按如图 1 所示的方式摆放,顶点 G 在直线 CD 上,边 GF 与直线 AB 交于点 H,若∠FHA=80°,则∠EGD=
(2)小亮将三角尺按如图 2 所示的方式摆放,顶点 F,G 分别在直线 AB,CD 上,∠FEG 的平分线与∠FGC 的平分线交于点 M,若∠EGD=4∠BFE,求∠M 的度数;
(3)小颖将图 2 中的三角尺进行适当转动,顶点 F,G 仍然分别在直线 AB,CD 上,如图 3,再将∠DGE 沿边 GE 翻折,边 GD 的对应边 GN 与直线 AB 交于点 N,小颖给出下列两个结论:
①∠CGN+∠BFE 的值不变;② $\frac{∠CGN}{∠BFE}$ 的值不变. 其中只有一个是正确的,你认为是哪个? 请说明理由.
(1)小明将三角尺按如图 1 所示的方式摆放,顶点 G 在直线 CD 上,边 GF 与直线 AB 交于点 H,若∠FHA=80°,则∠EGD=
40°
;(2)小亮将三角尺按如图 2 所示的方式摆放,顶点 F,G 分别在直线 AB,CD 上,∠FEG 的平分线与∠FGC 的平分线交于点 M,若∠EGD=4∠BFE,求∠M 的度数;
(3)小颖将图 2 中的三角尺进行适当转动,顶点 F,G 仍然分别在直线 AB,CD 上,如图 3,再将∠DGE 沿边 GE 翻折,边 GD 的对应边 GN 与直线 AB 交于点 N,小颖给出下列两个结论:
①∠CGN+∠BFE 的值不变;② $\frac{∠CGN}{∠BFE}$ 的值不变. 其中只有一个是正确的,你认为是哪个? 请说明理由.
答案：
24.
(1)$40^{\circ}$【解析】$\because \angle FHA = 80^{\circ}$，$AB// CD$，$\therefore \angle CGH = \angle FHA = 80^{\circ}$。$\because \angle EGF = 60^{\circ}$，$\therefore \angle EGD = 180^{\circ} - 60^{\circ} - 80^{\circ} = 40^{\circ}$。
(2)如图，过点$E$作$EK// AB$。
$\because AB// CD$，$\therefore AB// EK// CD$，$\therefore \angle BFE = \angle KEF$，$\angle KEG = \angle EGD$。$\because \angle KEF + \angle KEG = \angle FEG = 90^{\circ}$，$\therefore \angle BFE + \angle EGD = 90^{\circ}$。又$\angle EGD = 4\angle BFE$，$\therefore \angle BFE = 18^{\circ}$，$\angle EGD = 72^{\circ}$。$\because \angle EGF = 60^{\circ}$，$\therefore \angle FGC = 180^{\circ} - 60^{\circ} - 72^{\circ} = 48^{\circ}$。$\because EM$平分$\angle FEG$，$GM$平分$\angle FGC$，$\therefore \angle GEM = \frac{1}{2}×90^{\circ} = 45^{\circ}$，$\angle MGF = \frac{1}{2}×48^{\circ} = 24^{\circ}$，$\therefore \angle M = 180^{\circ} - \angle GEM - \angle EGF - \angle MGF = 180^{\circ} - 45^{\circ} - 60^{\circ} - 24^{\circ} = 51^{\circ}$。
(3)结论“$\frac{\angle CGN}{\angle BFE}$的值不变”正确，理由如下：设$\angle DGE = \angle NGE = x^{\circ}$，则$\angle CGN = 180^{\circ} - 2x^{\circ}$。由
(2)知$\angle BFE + \angle DGE = \angle FEG = 90^{\circ}$，$\therefore \angle BFE = 90^{\circ} - x^{\circ}$，$\therefore \frac{\angle CGN}{\angle BFE} = \frac{180^{\circ} - 2x^{\circ}}{90^{\circ} - x^{\circ}} = 2$，$\angle CGN + \angle BFE = 270^{\circ} - 3x^{\circ}$，$\therefore \angle CGN + \angle BFE$的值变化，$\frac{\angle CGN}{\angle BFE}$的值不变。
24.
(1)$40^{\circ}$【解析】$\because \angle FHA = 80^{\circ}$，$AB// CD$，$\therefore \angle CGH = \angle FHA = 80^{\circ}$。$\because \angle EGF = 60^{\circ}$，$\therefore \angle EGD = 180^{\circ} - 60^{\circ} - 80^{\circ} = 40^{\circ}$。
(2)如图，过点$E$作$EK// AB$。
$\because AB// CD$，$\therefore AB// EK// CD$，$\therefore \angle BFE = \angle KEF$，$\angle KEG = \angle EGD$。$\because \angle KEF + \angle KEG = \angle FEG = 90^{\circ}$，$\therefore \angle BFE + \angle EGD = 90^{\circ}$。又$\angle EGD = 4\angle BFE$，$\therefore \angle BFE = 18^{\circ}$，$\angle EGD = 72^{\circ}$。$\because \angle EGF = 60^{\circ}$，$\therefore \angle FGC = 180^{\circ} - 60^{\circ} - 72^{\circ} = 48^{\circ}$。$\because EM$平分$\angle FEG$，$GM$平分$\angle FGC$，$\therefore \angle GEM = \frac{1}{2}×90^{\circ} = 45^{\circ}$，$\angle MGF = \frac{1}{2}×48^{\circ} = 24^{\circ}$，$\therefore \angle M = 180^{\circ} - \angle GEM - \angle EGF - \angle MGF = 180^{\circ} - 45^{\circ} - 60^{\circ} - 24^{\circ} = 51^{\circ}$。(3)结论“$\frac{\angle CGN}{\angle BFE}$的值不变”正确，理由如下：设$\angle DGE = \angle NGE = x^{\circ}$，则$\angle CGN = 180^{\circ} - 2x^{\circ}$。由
(2)知$\angle BFE + \angle DGE = \angle FEG = 90^{\circ}$，$\therefore \angle BFE = 90^{\circ} - x^{\circ}$，$\therefore \frac{\angle CGN}{\angle BFE} = \frac{180^{\circ} - 2x^{\circ}}{90^{\circ} - x^{\circ}} = 2$，$\angle CGN + \angle BFE = 270^{\circ} - 3x^{\circ}$，$\therefore \angle CGN + \angle BFE$的值变化，$\frac{\angle CGN}{\angle BFE}$的值不变。
查看更多完整答案，请扫码查看
