2025年全优标准卷八年级数学上册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年全优标准卷八年级数学上册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
9. 如图,在△ABC 中,∠A=58°,P 为△ABC 内一点,过点 P 作直线 EF 分别交 AB,AC 于点 E,F.若点 E,F 分别在 PB,PC 的垂直平分线上,则∠BPC 的度数为(
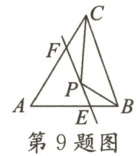
A.122°
B.120°
C.119°
D.116°
C
)
A.122°
B.120°
C.119°
D.116°
答案:
9.C
10. 如图,在△ABC 中,AB=AC,D,E 是△ABC 内两点,连接 AD,DE 和 BE,AD 平分∠BAC,∠EBC=∠E=60°,若 BE=6,DE=2,则 BC 的长度是(
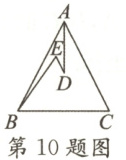
A.8
B.9
C.10
D.11
A
)
A.8
B.9
C.10
D.11
答案:
10.A
11. 已知某三角形的两边长分别为 2 和 5,第三边的长为偶数,则第三边的长为
4或6
。
答案:
11.4或6
12. 如图,△ABC≌△ADE,且 AE//BD,∠ADB=45°,则∠BAC 的度数为
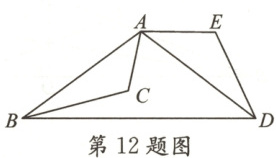
45°
。
答案:
12.45°
13. 如图,在△ABC 中,∠C=90°,E 是 AC 上一点,连接 BE,过点 E 作 ED⊥AB,垂足为点 D,BD=BC,若 AC=14 cm,则 AE+DE 的长度为
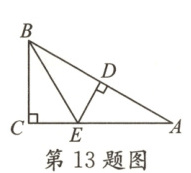
14cm
。
答案:
13.14cm
14. 如图,在正五边形 ABCDE 的内部,以 CD 为边作正方形 CDFH,连接 BH,则∠BHC=
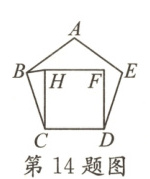
81
°。
答案:
14.81
15. △ABC 和△EDB 的位置如图所示,DE 交 AC 于点 F,BD=BC,BE=CA,∠DBE=∠C=60°,∠BDE=75°,则∠AFD 的度数为
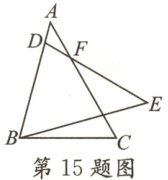
30
°。
答案:
15.30
16. (6 分)如图,AB=CD,AE⊥BC,DF⊥BC,垂足分别为点 E,F,且 CE=BF.求证:AB//CD.
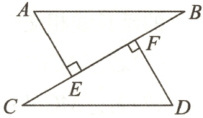

答案:
16.证明:
∵AE⊥BC,DF⊥BC,
∴∠DFC=∠AEB=90°.
∵CE=BF,
∴CE+EF=BF+EF,
即CF=BE.
在Rt△DFC和Rt△AEB中,$\begin{cases} CF=BE, \\ CD=BA, \end{cases}$
∴Rt△DFC≌Rt△AEB(HL),
∴∠B=∠C,
∴AB//CD.
∵AE⊥BC,DF⊥BC,
∴∠DFC=∠AEB=90°.
∵CE=BF,
∴CE+EF=BF+EF,
即CF=BE.
在Rt△DFC和Rt△AEB中,$\begin{cases} CF=BE, \\ CD=BA, \end{cases}$
∴Rt△DFC≌Rt△AEB(HL),
∴∠B=∠C,
∴AB//CD.
17. (6 分)如图,在△ABC 中,∠B=46°,∠C=80°,AD⊥BC 于点 D,AE 平分∠BAC 交 BC 于点 E,DF⊥AE 于点 F.
(1)求∠BAE 的度数;
(2)求∠ADF 的度数.
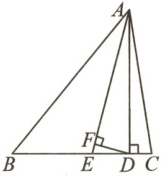
(1)求∠BAE 的度数;
(2)求∠ADF 的度数.

答案:
17.解:
(1)
∵∠B=46°,∠C=80°,
∴∠BAC=180°−∠B−∠C=54°.
∵AE平分∠BAC,
∴∠BAE=∠CAE=$\frac{1}{2}$∠BAC=27°.
(2)
∵AD⊥BC,
∴∠ADC=90°.
∵∠C=80°,
∴∠DAC=90°−∠C=10°.
∵∠CAE=27°,
∴∠DAE=∠CAE−∠DAC=27°−10°=17°.
∵DF⊥AE,
∴∠AFD=90°,
∴∠ADF=90°−∠DAE=90°−17°=73°.
(1)
∵∠B=46°,∠C=80°,
∴∠BAC=180°−∠B−∠C=54°.
∵AE平分∠BAC,
∴∠BAE=∠CAE=$\frac{1}{2}$∠BAC=27°.
(2)
∵AD⊥BC,
∴∠ADC=90°.
∵∠C=80°,
∴∠DAC=90°−∠C=10°.
∵∠CAE=27°,
∴∠DAE=∠CAE−∠DAC=27°−10°=17°.
∵DF⊥AE,
∴∠AFD=90°,
∴∠ADF=90°−∠DAE=90°−17°=73°.
查看更多完整答案,请扫码查看


