《2025年全优标准卷八年级数学上册人教版》

18. (8 分)如图,在平面直角坐标系中,△ABC 三个顶点的坐标分别为 A(−3,1),B(−4,−1),C(0,2).
(1)以 y 轴为对称轴,画出△ABC 的轴对称图形△DEF(其中点 D,E,F 分别是点 A,B,C 的对应点)；
(2)写出△DEF 的顶点坐标.

答案：
18.解:
(1)如图所示，△DEF即为所求作三角形.　　　　　　　
　　　　　
(2)D(3,1),E(4,−1),F(0,2).

19. (8 分)如图,AD 是△ABC 的高,CE 是△ABC 的角平分线,BF 是△ABC 的中线.
(1)若∠ACB=50°,∠BAD=65°,求∠AEC 的度数；
(2)若 AB=9,△BCF 与△BAF 的周长差为 3,求 BC 的长.

答案： 19.解:
(1)
∵AD是△ABC的高，
∴∠ADB=90°.
∵∠BAD=65°,
∴∠ABD=90°−65°=25°.
∵CE是∠ACB的平分线，∠ACB=50°,
∴∠ECB=$\frac{1}{2}$∠ACB=25°,
∴∠AEC=∠ABD+∠ECB=25°+25°=50°.
(2)
∵F是AC的中点，
∴AF=FC;
∵△BCF与△BAF的周长差为3,
∴(BC+CF+BF)−(AB+AF+BF)=3,
∴BC−AB=3.
∵AB=9,
∴BC=12.

20. (8 分)如图,在△ABC 中,∠B=62°,∠BAC=76°,D 为 BC 上一点,DE 交 AC 于点 F,且 AB=AD=DE,连接 AE,∠E=55°.请判断△AFD 的形状,并说明理由.

答案： 20.解:△AFD是直角三角形.理由如下:
∵AB=AD,
∴∠ADB=∠B=62°,
∴∠BAD=180°−2×62°=56°,
∴∠DAC=76°−56°=20°.
∵AD=DE,
∴∠DAE=∠E=55°,
∴∠ADE=180°−2×55°=70°,
∴∠DAC+∠ADE=90°,
∴△AFD是直角三角形.

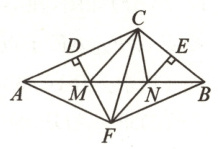
21. (8 分)如图,在△ABC 中,DM,EN 分别垂直平分 AC 和 BC,交 AB 于 M,N 两点,DM 与 EN 的延长线相交于点 F,连接 CM,CN.
(1)若∠ACB=110°,则∠MCN 的度数为40°；
(2)若∠MCN=α,则∠MFN 的度数为90°−$\frac{\alpha}{2}$；(用含α的代数式表示)
(3)连接 FA,FB,FC,已知△CMN 的周长为 6 cm,△FAB 的周长为 14 cm,求 FC 的长.

答案： 21.解:
(1)40° 【解析】
∵DM,EN分别垂直平分AC和BC,
∴AM=CM,BN=CN,
∴∠CAM=∠ACM,∠CBN=∠BCN.
∵∠CAM+∠CBN+∠ACM+∠BCN+∠MCN=180°,∠ACB=∠ACM+∠BCN+∠MCN=110°,
∴∠CAM+∠CBN=70°,
∴∠CAM+∠CBN+∠ACM+∠BCN=140°,
∴∠MCN=40°.
(2)90°−$\frac{\alpha}{2}$ 【解析】
∵DM,EN分别垂直平分AC和BC,
∴AM=CM,BN=CN,
∴∠CAM=∠ACM,∠CBN=∠BCN.
∵∠CAM+∠CBN+∠ACM+∠BCN+∠MCN=180°,∠MCN=α,
∴∠CAM+∠CBN=90°−$\frac{\alpha}{2}$,
∴∠ACB=90°+$\frac{\alpha}{2}$.
∵∠ACB+∠MFN=360°−90°−90°=180°,
∴∠MFN=90°−$\frac{\alpha}{2}$.
(3)
∵DM,EN分别垂直平分AC和BC，
∴AM=CM,BN=CN,
∴△CMN的周长=CM+MN+CN=AM+MN+BN=AB.
∵△CMN的周长为6cm,
∴AB=6cm.
∵△FAB的周长为14cm,
∴FA+FB+AB=14cm,
∴FA+FB=8cm.
∵DF,EF分别垂直平分AC和BC，
∴FA=FC,FB=FC,
∴2FC=8cm,
∴FC=4cm.