《2025年全优标准卷八年级数学上册人教版》

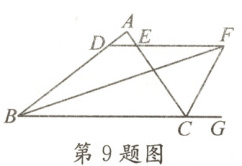
9. 如图,$\angle ABC$的平分线$BF$与$\triangle ABC$的外角$\angle ACG$的平分线相交于点$F$,过点$F$作$DF// BC$交$AB$于点$D$,交$AC$于点$E$,若$BD = 8$,$CE = 6$,则$DE$的长为(C)

A.$4$
B.$2.5$
C.$2$
D.$1.5$

答案： C

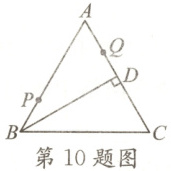
10. 如图,在等边三角形$ABC$中,$BD\perp AC$于点$D$,$QD = 1.5$,点$P$,$Q$分别为$AB$,$AD$上的两个定点,且$BP = AQ = 2$.若在$BD$上有一动点$E$使$PE + QE$的值最短,则$PE + QE$的最小值为(D)

A.$3.5$
B.$4$
C.$4.5$
D.$5$

答案： D

11. 若某等腰三角形的一个内角为$50^{\circ}$,则它的顶角的度数是50°或80°.

答案： 50°或80°

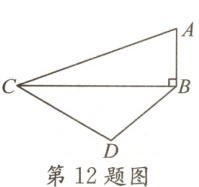
12. 如图,$AB\perp BC$,$\angle ACB = 20^{\circ}$,$\angle CBD = 40^{\circ}$,$AC = 4$,$BD = 2$,则$\angle BCD =$30°.

答案： 30°

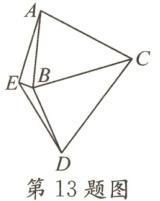
13. 如图,线段$AB$,$DE$的垂直平分线交于点$C$,且$\angle ABC = \angle EDC = 68^{\circ}$,$\angle AEB = 94^{\circ}$,则$\angle EBD$的度数为138°.

答案： 138°

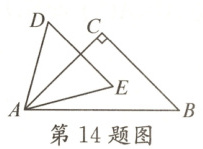
14. 如图,将一个等腰直角三角形$ABC$和一个等边三角形$ADE$的顶点$A$重合放在一起($AC ＞ AE$,$0^{\circ} ＜ \angle BAE ＜ 90^{\circ}$,且点$E$在直线$AB$的上方),其中$\angle C = 90^{\circ}$,$\angle B = 45^{\circ}$.当两个三角形有一组边互相平行时,$\angle BAE$的度数为15°或60°或75°.

答案： 15°或60°或75°

15. 一张台球桌的桌面如图所示,一个球从桌面的点$A$滚向桌边$PQ$,碰着$PQ$上的点$B$后便反弹而滚向桌边$RS$,碰着$RS$上的点$C$便反弹而滚入点$Q$,一共反弹两次.已知$AB$,$BC$,$CQ$都是直线,$PQ// RS$,且$\angle ABC$的平分线$BN$垂直于$PQ$,$\angle BCQ$的平分线$CM$垂直于$RS$,若$\angle CQR = 33^{\circ}$,则$\angle ABP$的度数为57°.

答案： 57°

16. (6 分)如图,在$\triangle ABC$中,$AB = AC$,$D$是边$AB$上一点,$\angle BCD = \angle A$.
(1)求证:$CD = CB$;
(2)如图,过点$B$作$BE\perp AC$于点$E$,试证明$\angle BCD = 2\angle CBE$.

答案： 证明:
(1)设∠BCD=∠A=α.
∵在△ABC中,AB=AC,
∴∠ABC=∠ACB=$\frac{1}{2}$(180°−∠A)=90°−$\frac{1}{2}$α,
∴∠ACD=∠ACB−∠BCD=$90°-\frac{1}{2}α-α=90°-\frac{3}{2}α$，
∴∠CDB=∠A+∠ACD=α+90°−$\frac{3}{2}$α=90°−$\frac{1}{2}$α,
∴∠ABC=∠CDB=90°−$\frac{1}{2}$α,
∴CD=CB.
(2)
∵BE⊥AC,
∴∠CBE=90°−∠ACB=$90°-(90°-\frac{1}{2}α)=\frac{1}{2}α$,
　又
∵∠BCD=∠A=α,
∴∠CBE=$\frac{1}{2}$∠BCD,
∴∠BCD=2∠CBE.