《2025年全优标准卷八年级数学上册人教版》

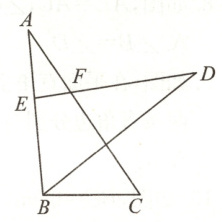
17. (6 分) 如图,$\triangle ABC\cong\triangle DEB$,点 $E$ 在边 $AB$ 上,$DE$ 与 $AC$ 相交于点 $F$.
(1) 若 $AE = 9$,$BC = 13$,求线段 $DE$ 的长;
(2) 若$\angle A = 37^{\circ}$,$\angle DBE = 50^{\circ}$,求$\angle EFC$ 的度数.

答案： 17.解:
(1)
∵△ABC≌△DEB,
∴DE=AB,BE=BC=13.
∵AB=AE+BE=9+13=22,
∴DE=22.
(2)
∵△ABC≌△DEB,
∴∠D=∠A=37°.
∵∠AFD=∠A+∠AEF,∠AEF=∠D+∠DBE,
∴∠AFD=∠A+∠D+∠DBE=37°+37°+50°=124°,
∴∠EFC=∠AFD=124°.

18. (7 分) 如图,在$\triangle ABC$ 中,$\angle B = 90^{\circ}$,$AD$ 是$\angle BAC$ 的平分线,$DM\perp AC$于点 $M$,点 $N$ 在边 $AB$ 上,且 $DN = DC$.
(1) 求证:$BN = CM$;
(2) 试判断 $AC$ 与 $AN$,$CM$ 之间存在的数量关系,并说明理由.

答案： 18.
(1)证明:
∵在△ABC中,∠B=90°,
∴BD⊥AB.
∵DM⊥AC于点M,且AD是∠BAC的平分线，
∴BD=DM. 在Rt△BDN和Rt△MDC中，$\begin{cases}BD=MD,\\DN=DC,\end{cases} $
∴Rt△BDN≌Rt△MDC(HL),
∴BN=CM.
(2)解:AC=AN+2CM,理由如下:
∵在Rt△ABD和Rt△AMD中，$\begin{cases}BD=MD,\\AD=AD,\end{cases} $
∴Rt△ABD≌Rt△AMD(HL),
∴AB=AM,
∴AC=AM+CM=AB+CM=AN+BN+CM. 由
(1)得BN=CM,
∴AC=AN+2CM.

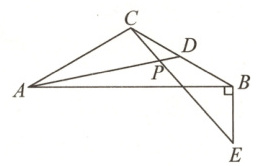
19. (7 分) 如图,在$\triangle ABC$ 中,$AC = BC$,$\angle CAB=\angle CBA = 30^{\circ}$,$BE\perp AB$,$D$ 为 $BC$ 上一点,且 $CD = BE$,$AD$,$CE$ 交于点 $P$.
(1) 求证:$\triangle ACD\cong\triangle CBE$;
(2) 猜想$\angle APC$ 的度数,并说明理由.

答案： 19.
(1)证明:
∵∠CAB=∠CBA=30°,
∴∠ACB=180°-30°-30°=120°.
∵BE⊥AB,
∴∠ABE=90°,
∴∠CBE=∠CBA+∠ABE=120°,
∴∠ACD=∠CBE. 在△ACD和△CBE中，$\begin{cases}AC=CB,\\∠ACD=∠CBE,\\CD=BE,\end{cases} $
∴△ACD≌△CBE(SAS).
(2)解:∠APC=60°,理由如下:
∵△ACD≌△CBE,
∴∠CAD=∠BCE,
∴∠APC=∠PCD+∠PDC=∠CAD+∠PDC=180°-∠ACD=60°.

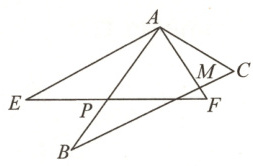
20. (8 分) 如图,$\triangle ABC\cong\triangle AEF$,$\angle EAB = 25^{\circ}$,$\angle F = 57^{\circ}$.
(1) 求证:$\angle EAB=\angle CAF$;
(2) $\triangle ABC$ 可以经过图形的变换得到$\triangle AEF$,请你描述这个变换;
(3) 求$\angle AMB$ 的度数.

答案： 20.
(1)证明:
∵△ABC≌△AEF,
∴∠BAC=∠EAF,
∴∠EAB+∠BAF=∠CAF+∠BAF,
∴∠EAB=∠CAF.
(2)
∵∠EAB=25°,△ABC≌△AEF,
∴△ABC绕点A顺时针旋转25°,可以得到△AEF.
(3)解:由
(1)知∠EAB=∠CAF=25°.
∵△ABC≌△AEF,
∴∠C=∠F=57°,
∴∠AMB=∠C+∠CAF=57°+25°=82°.

21. (8 分) 小明与爸爸妈妈在操场上荡秋千. 小明坐在秋千上的起始位置 $A$ 处,起始位置 $OA$ 与地面垂直,小明两脚在地面上用力一蹬,妈妈在距地面 $1.2\,m$ 高的 $B$ 处接住他,妈妈用力一推,爸爸在 $C$ 处接住他. 妈妈与爸爸到秋千起始位置 $OA$ 的水平距离 $BF$,$CG$ 分别为 $1.8\,m$ 和 $2.2\,m$,$\angle BOC = 90^{\circ}$.
(1) $\triangle CGO$ 与$\triangle OFB$ 全等吗? 请说明理由;
(2) 请直接写出爸爸在距离地面多高的地方接住小明.

答案： 21.解:
(1)△CGO与△OFB全等.理由如下: 由题意,得∠BFO=∠OGC=90°,OB=OC.
∵∠BOC=90°,
∴∠COG+∠BOF=90°=∠BOF+∠OBF,
∴∠COG=∠OBF. 在△CGO和△OFB中，$\begin{cases}∠COG=∠OBF,\\∠CGO=∠OFB,\\OC=BO,\end{cases} $
∴△CGO≌△OFB(AAS).
(2)
∵△CGO≌△OFB,
∴CG=OF,OG=BF.
∵BF=1.8m,CG=2.2m,
∴FG=OF - OG=CG - BF=2.2 - 1.8=0.4(m). 由题意，得点F距离地面1.2m,则点G到地面的距离=1.2+FG=1.2+0.4=1.6(m), 即爸爸是在距离地面1.6m的地方接住小明的.