《2025年全优标准卷八年级数学上册人教版》

$22. (13 $分$)$我们已经知道$,$对于一个图形$,$通过用不同的方法计算图形的面积可以得到一个数学等式$.$请结合图形解答下列问题$.$　　
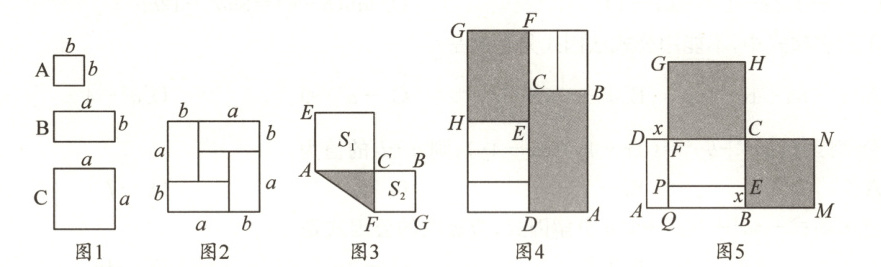
$(1)$利用若干张图$ 1 $中的$ A,B,C $三种纸片$,$拼成一个$“$回形$”$正方形$($如图$ 2),$请你写出$(a + b)^{2},(a - b)^{2}$和$ab$之间的数量关系$:$　　$(a+b)^2=(a-b)^2+4ab$　　$;$　　
$(2)$根据$(1)$的结论$,$若$x + y = 4,xy = 1,$则$(x - y)^{2}$的值是　　$12$　　$;$　　
$(3)$如图$ 3,C $是线段$AB$上的一点$,$分别以$AC,BC$为边向两边作正方形$,$设$AB = 6,$两正方形的面积和$S_{1}+S_{2}=18,$求图中阴影部分面积$;$　　
$(4)$利用$5$张$ B $种纸片拼成如图$ 4 $所示的大长方形$,$记长方形$ABCD$的面积为$S_{1},$长方形$EFGH$的面积为$S_{2}.$设$CD = x,$若当$x$取不同数值时$,S_{1}-S_{2}$永远为定值$,$则$a$与$b$之间的数量关系为　　$a=2b$　　$;$　　
$(5)$如图$ 5,$在长方形$ABCD$中$,AB = 22\ cm,E,F$分别是边$BC,CD$上的点$,EC = 10\ cm,$且$BE = DF = x\ cm,$分别以$FC,CB$为边在长方形$ABCD$外侧作正方形$CFGH$和正方形$CBMN,$若长方形$CBQF$的面积为$300\ cm^{2},$求图中阴影部分的面积之和$.$　　

答案： 22.解：$(1)(a+b)^2=(a-b)^2+4ab【$解析】大正方形的边长为a+b，因此面积为$(a+b)^2；$中间小正方形的边长为a-b，因此面积为$(a-b)^2；$周围4个长方形的面积和为4ab，因此有$(a+b)^2=(a-b)^2+4ab.$
(2)12【解析】
∵x+y=4,xy=1，
∴$(x-y)^2=(x+y)^2-4xy=16-4=12.$
(3)设两个正方形的边长分别为a,b,a＞b＞0，
则$a+b=6,a^2+b^2=S_1+S_2=18，$
∴S_阴影部分$=1/2ab=1/2×[(a+b)^2-(a^2+b^2)]=1/2×36-18/2=9/2.$
(4)a=2b【解析】长方形ABCD的长为x，宽为2b，因此面积$S_1=2bx，$
长方形EFGH的长为x+a-3b，宽为a，因此面积$S_2=a(x+a-3b)，$
∴$S_1-S_2=2bx-a(x+a-3b)=(2b-a)x-a^2+3ab.$
∵$S_1-S_2$永远为定值，
∴2b-a=0，即a=2b.
(5)
∵在长方形ABCD中，AB=22cm，BE=DF=x,EC=10cm，
∴CF=AB-DF=(22-x)cm,BC=BE+CE=(x+10)cm.
∵长方形CBQF的面积为$300cm^2，$
∴(22-x)(x+10)=300.
设正方形FCHG的边长为acm，正方形BCNM的边长为bcm，
则a=22-x,b=x+10，
∴a+b=32,ab=300，
∴S_阴影部分$=a^2+b^2=(a+b)^2-2ab=32^2-2×300=424(cm^2)，$
即图中阴影部分的面积之和为$424cm^2.$