2025年全优标准卷八年级数学上册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年全优标准卷八年级数学上册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
18. (7 分)如图,AD 为△ABC 的角平分线,P 为 AD 上的点,过点 P 作 PE⊥AD 交 BC 的延长线于点 E. 若∠B=30°,∠ACB=80°,求∠E 的度数.


答案:
18.解:$\because \angle B = 30^{\circ}$,$\angle ACB = 80^{\circ}$,$\therefore \angle BAC = 180^{\circ} - 30^{\circ} - 80^{\circ} = 70^{\circ}$。$\because AD$为$\triangle ABC$的角平分线,$\therefore \angle BAD = \frac{1}{2}\angle BAC = 35^{\circ}$,$\therefore \angle ADC = \angle B + \angle BAD = 30^{\circ} + 35^{\circ} = 65^{\circ}$。$\because PE\perp AD$,$\therefore \angle DPE = 90^{\circ}$,在$Rt\triangle DEP$中,$\angle E = 90^{\circ} - 65^{\circ} = 25^{\circ}$。
19. (8 分)如图,在△ABC 中,点 D,E 分别在 AB,AC 上. 已知 DE//BC,∠EDC=40°,∠AED=80°.
(1)求证:CD 平分∠ACB;
(2)过点 B 作∠ABC 的平分线交 CD 于点 F,若∠A=52°,求∠BFD 的度数.

(1)求证:CD 平分∠ACB;
(2)过点 B 作∠ABC 的平分线交 CD 于点 F,若∠A=52°,求∠BFD 的度数.

答案:
19.
(1)证明:$\because DE// BC$,$\angle EDC = 40^{\circ}$,$\angle AED = 80^{\circ}$,$\therefore \angle BCD = \angle EDC = 40^{\circ}$,$\angle ACB = \angle AED = 80^{\circ}$,$\therefore \angle ACB = 2\angle BCD$,$\therefore CD$平分$\angle ACB$。
(2)解:$\because$在$\triangle ADE$中,$\angle A = 52^{\circ}$,$\angle AED = 80^{\circ}$,$\therefore \angle ADE = 180^{\circ} - \angle A - \angle AED = 180^{\circ} - 52^{\circ} - 80^{\circ} = 48^{\circ}$,$\therefore \angle ADC = \angle ADE + \angle EDC = 48^{\circ} + 40^{\circ} = 88^{\circ}$。$\because DE// BC$,$\therefore \angle ABC = \angle ADE = 48^{\circ}$。$\because BF$平分$\angle ABC$,$\therefore \angle DBF = \frac{1}{2}\angle ABC = \frac{1}{2}×48^{\circ} = 24^{\circ}$。$\because \angle ADC$是$\triangle BDF$的外角,$\therefore \angle BFD = \angle ADC - \angle DBF = 88^{\circ} - 24^{\circ} = 64^{\circ}$。
(1)证明:$\because DE// BC$,$\angle EDC = 40^{\circ}$,$\angle AED = 80^{\circ}$,$\therefore \angle BCD = \angle EDC = 40^{\circ}$,$\angle ACB = \angle AED = 80^{\circ}$,$\therefore \angle ACB = 2\angle BCD$,$\therefore CD$平分$\angle ACB$。
(2)解:$\because$在$\triangle ADE$中,$\angle A = 52^{\circ}$,$\angle AED = 80^{\circ}$,$\therefore \angle ADE = 180^{\circ} - \angle A - \angle AED = 180^{\circ} - 52^{\circ} - 80^{\circ} = 48^{\circ}$,$\therefore \angle ADC = \angle ADE + \angle EDC = 48^{\circ} + 40^{\circ} = 88^{\circ}$。$\because DE// BC$,$\therefore \angle ABC = \angle ADE = 48^{\circ}$。$\because BF$平分$\angle ABC$,$\therefore \angle DBF = \frac{1}{2}\angle ABC = \frac{1}{2}×48^{\circ} = 24^{\circ}$。$\because \angle ADC$是$\triangle BDF$的外角,$\therefore \angle BFD = \angle ADC - \angle DBF = 88^{\circ} - 24^{\circ} = 64^{\circ}$。
20. (8 分)已知△ABC 的三边长分别为 a,b,c,且 a,b,c 都是整数.
(1)若 a=2,b=5,且 c 为偶数,求△ABC 的周长;
(2)化简:|a - b + c| - |b - c - a| + |a + b + c|.
(1)若 a=2,b=5,且 c 为偶数,求△ABC 的周长;
(2)化简:|a - b + c| - |b - c - a| + |a + b + c|.
答案:
20.
(1)解:$\because a = 2$,$b = 5$,$\therefore 5 - 2 < c < 5 + 2$,$\therefore 3 < c < 7$。$\because c$为偶数,$\therefore c = 4$或6。当$c = 4$时,$\triangle ABC$的周长$= a + b + c = 2 + 5 + 4 = 11$;当$c = 6$时,$\triangle ABC$的周长$= a + b + c = 2 + 5 + 6 = 13$。综上所述,$\triangle ABC$的周长为11或13。
(2)解:$\because \triangle ABC$的三边长为$a$,$b$,$c$,$\therefore a + c > b$,$\therefore |a - b + c| - |b - c - a| + |a + b + c| = a + c - b - (a + c - b) + a + b + c = a + c - b - a - c + b + a + b + c = a + b + c$。
(1)解:$\because a = 2$,$b = 5$,$\therefore 5 - 2 < c < 5 + 2$,$\therefore 3 < c < 7$。$\because c$为偶数,$\therefore c = 4$或6。当$c = 4$时,$\triangle ABC$的周长$= a + b + c = 2 + 5 + 4 = 11$;当$c = 6$时,$\triangle ABC$的周长$= a + b + c = 2 + 5 + 6 = 13$。综上所述,$\triangle ABC$的周长为11或13。
(2)解:$\because \triangle ABC$的三边长为$a$,$b$,$c$,$\therefore a + c > b$,$\therefore |a - b + c| - |b - c - a| + |a + b + c| = a + c - b - (a + c - b) + a + b + c = a + c - b - a - c + b + a + b + c = a + b + c$。
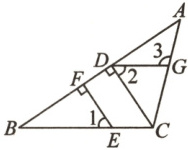
21. (8 分)如图,在△ABC 中,CD⊥AB,垂足为点 D,点 E 在 BC 上,EF⊥AB,垂足为点 F,G 为 AC 上一点,连接 DG. 已知∠1=∠2.
(1)求证:DG//BC;
(2)如果∠B=54°,且∠ACD=35°,求∠3 的度数.
(1)求证:DG//BC;
(2)如果∠B=54°,且∠ACD=35°,求∠3 的度数.

答案:
21.
(1)证明:$\because CD\perp AB$,$EF\perp AB$,$\therefore CD// EF$,$\therefore \angle1 = \angle BCD$。又$\because \angle1 = \angle2$,$\therefore \angle2 = \angle BCD$,$\therefore DG// BC$。
(2)解:$\because EF\perp AB$,$\therefore \angle BFE = 90^{\circ}$。又$\angle B = 54^{\circ}$,$\therefore \angle1 = 36^{\circ}$,$\therefore \angle BCD = \angle1 = 36^{\circ}$。$\because BC// DG$,$\therefore \angle3 = \angle ACB = \angle ACD + \angle BCD = 35^{\circ} + 36^{\circ} = 71^{\circ}$。
(1)证明:$\because CD\perp AB$,$EF\perp AB$,$\therefore CD// EF$,$\therefore \angle1 = \angle BCD$。又$\because \angle1 = \angle2$,$\therefore \angle2 = \angle BCD$,$\therefore DG// BC$。
(2)解:$\because EF\perp AB$,$\therefore \angle BFE = 90^{\circ}$。又$\angle B = 54^{\circ}$,$\therefore \angle1 = 36^{\circ}$,$\therefore \angle BCD = \angle1 = 36^{\circ}$。$\because BC// DG$,$\therefore \angle3 = \angle ACB = \angle ACD + \angle BCD = 35^{\circ} + 36^{\circ} = 71^{\circ}$。
查看更多完整答案,请扫码查看


