《2025年全优标准卷八年级数学上册人教版》

14. 已知$x^{2}-2x = 2$,则代数式$(x - 1)^{2}+2022=$2025。

答案： 14.2025

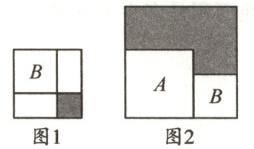
15. 有两个正方形$A,B$,现将$B$放在$A$的内部得图 1,将$A,B$并列放置后构造新的正方形得图 2.若图 1 和图 2 中阴影部分的面积分别为 4 和 18,则图 2 所示的大正方形的面积为40。

答案： 15.40

16. (6 分)在计算$(3x + a)(x + b)$时,甲错把$b$看成了 6,得到的结果是$3x^{2}+9x - 54$;乙错把$a$看成了$-a$,得到的结果是$3x^{2}+21x + 36$.求$a + b$的值.

答案： 16.解：
∵甲错把$b$看成了6，得到的结果是$3x^{2}+9x-54$，
$\therefore (3x+a)(x+6)=3x^{2}+(a+18)x+6a=3x^{2}+9x-54$。
∵乙错把$a$看成了一$a$，得到的结果是$3x^{2}+21x+36$，
$\therefore (3x-a)(x+b)=3x^{2}+(-a+3b)x-ab=3x^{2}+21x+36$，
$\therefore \begin{cases}a+18=9,\\-a+3b=21,\end{cases}$解得$\begin{cases}a=-9,\\b=4,\end{cases}$
$\therefore a+b=-9+4=-5$。

17. (6 分)已知$m - n = 5,mn = 2$,求下列各式的值:
(1)$(m + n)^{2}$;
(2)$5m^{2}+5n^{2}-3mn$.

答案： 17.解：
(1)
∵$m-n=5$，$mn=2$，
$\therefore (m+n)^{2}=(m-n)^{2}+4mn=25+4×2=33$。
(2)
∵$(m+n)^{2}=33$，$mn=2$，
$\therefore m^{2}+n^{2}=(m+n)^{2}-2mn=33-4=29$，
$\therefore 5m^{2}+5n^{2}-3mn=5(m^{2}+n^{2})-3mn=5×29-$
$3×2=145-6=139$。

18. (6 分)计算:
(1)$(x - 3y)^{2}$;
(2)$(2x + y)^{2}(y - 2x)^{2}$.

答案： 18.解：
(1)原式=$x^{2}-6xy+9y^{2}$.
(2)原式=$[(2x+y)(y-2x)]^{2}=(y^{2}-4x^{2})^{2}=$
$y^{4}-8x^{2}y^{2}+16x^{4}$。

19. (8 分)已知$n$为正整数,且$x^{2n}=4$.求下列各式的值:
(1)$x^{n}$;
(2)$(x^{3n})^{2}+2(x^{2})^{2n}$.

答案： 19.解：
(1)
∵$x^{2n}=(x^{n})^{2}$，$x^{n}=±2$.
(2)原式=$(x^{2n})^{3}+2(x^{2n})^{2}=4^{3}+2×4^{2}=64+$
$32=96$。