《2025年全优标准卷八年级数学上册人教版》

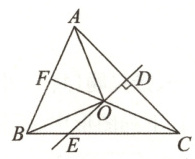
22. (8 分)如图,在$\triangle ABC$中,$AC = BC$,$F$为$AB$的中点,$AC$的垂直平分线分别交$AC$,$CF$,$CB$于点$D$,$O$,$E$,连接$OA$,$OB$.
(1) 求证:$\triangle OBC$为等腰三角形;
(2) 若$\angle ACF = 25^{\circ}$,求$\angle BOE$的度数.

答案： 22.
(1)证明：$\because DE$为$AC$的垂直平分线，
$\therefore OC=OA$.
$\because AC=BC$，$F$为$AB$的中点，
$\therefore CF$为$AB$的垂直平分线，$\therefore OB=OA$，
$\therefore OB=OC$，$\therefore \triangle OBC$为等腰三角形.
(2)解：$\because AC=BC$，$F$为$AB$的中点，
$\therefore CF$为$\angle ACB$的平分线，
$\therefore \angle ACF=\angle BCF=\frac{1}{2}\angle ACB=25^{\circ}$，
$\therefore \angle ACB=50^{\circ}$，$\therefore \angle DEC=180^{\circ}-\angle EDC-\angle ACB=180^{\circ}-90^{\circ}-50^{\circ}=40^{\circ}$.
$\because \triangle OBC$为等腰三角形，
$\therefore \angle CBO=\angle BCF=25^{\circ}$，
$\therefore \angle BOE=\angle DEC-\angle CBO=40^{\circ}-25^{\circ}=15^{\circ}$.

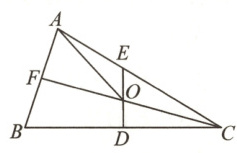
23. (11 分)如图,在$\triangle ABC$中,$AB = 6$,$AC = 10$,$CF$平分$\angle ACB$,$D$是$BC$的中点,$E$是$AC$上一点,连接$DE$交$CF$于点$O$.
(1) 若$\triangle CDE$的周长与四边形$ABDE$的周长相等,求$AE$的长;
(2) 若$AC = BC$,$DE\perp BC$,$\angle ACB = \beta$,连接$OA$.
① 求证:点$O$在线段$AC$的垂直平分线上;
② 求$\angle AOE$的度数.(用含$\beta$的式子表示)

答案：
23.
(1)解：$\because D$是$BC$的中点，$\therefore BD=CD$.
$\because \triangle CDE$的周长与四边形$ABDE$的周长相等，
$\therefore CD+DE+CE=BD+DE+AB+AE$，
$\therefore CE=AB+AE$.
$\because AB=6$，$AC=10$，
$\therefore CE=6+10 - CE$，$\therefore CE=8$，
$\therefore AE=10 - CE=2$.
(2)①证明：如图，连接$OB$.

$\because DE\perp BC$，$D$是$BC$的中点，$\therefore OB=OC$.
$\because CF$平分$\angle ACB$，$AC=BC$，$\therefore CF$垂直平分$AB$，
$\therefore OA=OB$，$\therefore OA=OC$，
$\therefore$点$O$在线段$AC$的垂直平分线上.
②解：$\because DE\perp BC$，$\therefore \angle CDE=90^{\circ}$，$\therefore \angle CED=90^{\circ}-\angle ACB=90^{\circ}-\beta$.
$\because CF$平分$\angle ACB$，$\angle ACB=\beta$，
$\therefore \angle ACO=\frac{1}{2}\angle ACB=\frac{1}{2}\beta$.
$\because OA=OC$，$\therefore \angle CAO=\angle ACO=\frac{1}{2}\beta$，
$\therefore \angle AOE=\angle CEO-\angle CAO=90^{\circ}-\beta-\frac{1}{2}\beta=90^{\circ}-\frac{3}{2}\beta$.

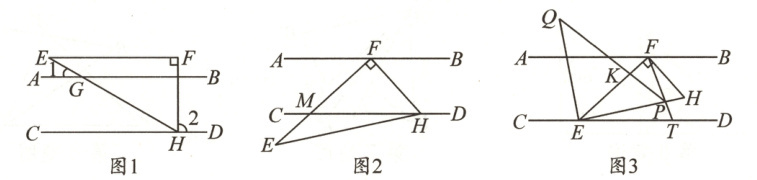
24. (12 分)已知:直线$AB// CD$,在三角尺$EFH$中,$\angle EFH = 90^{\circ}$,$\angle EHF = 60^{\circ}$.
(1) 如图 1,三角尺$EFH$的顶点$H$落在直线$CD$上,且$EH$与直线$AB$相交于点$G$,若$\angle 2 = 3\angle 1$,求$\angle 1$的度数;
(2) 如图 2,当三角尺$EFH$的顶点$F$落在直线$AB$上,且顶点$H$仍在直线$CD$上时,$EF$与直线$CD$相交于点$M$,试确定$\angle E$,$\angle AFE$,$\angle MHE$的数量关系;
(3) 如图 3,当三角尺$EFH$的顶点$F$落在直线$AB$上,且顶点$H$在$AB$,$CD$之间,而顶点$E$恰好落在直线$CD$上时,在线段$EH$上取点$P$,连接$FP$并延长交直线$CD$于点$T$,在线段$EF$上取点$K$,连接$PK$并延长交$\angle CEH$的平分线于点$Q$,若$\angle Q-\angle HFT = 15^{\circ}$,且$\angle EFT = \angle ETF$.
① 试探求$\angle HFT$与$\angle AFE$之间的数量关系,并说明理由;
② 求证:$PQ// FH$.

答案： 24.
(1)解：$\because AB// CD$，$\therefore \angle1=\angle CHG$.
$\because \angle2=3\angle1$，$\therefore \angle2=3\angle CHG$.
$\because \angle CHG+\angle EHF+\angle2=180^{\circ}$，
$\therefore 4\angle CHG+60^{\circ}=180^{\circ}$，$\therefore \angle CHG=30^{\circ}$，
$\therefore \angle1=30^{\circ}$.
(2)解：$\angle AFE=\angle E+\angle MHE$，理由如下：
$\because AB// CD$，$\therefore \angle AFE=\angle CME$.
$\because \angle CME=\angle E+\angle MHE$，
$\therefore \angle AFE=\angle E+\angle MHE$.
(3)设$\angle AFE=x$，
则$\angle BFH=90^{\circ}-x$，$\angle EFB=180^{\circ}-x$.
①解：$\because AB// CD$，$\therefore \angle BFT=\angle ETF$.
$\because \angle EFT=\angle ETF$，
$\therefore \angle EFT=\angle BFT=\frac{1}{2}\angle EFB=90^{\circ}-\frac{1}{2}x$，
$\therefore \angle HFT=\angle BFT-\angle BFH=\frac{1}{2}x$，
即$\angle HFT=\frac{1}{2}\angle AFE$.
②证明：$\because \angle Q-\angle HFT=15^{\circ}$，
$\therefore \angle Q=15^{\circ}+\frac{1}{2}x$.
$\because AB// CD$，$\therefore \angle AFE+\angle CEF=180^{\circ}$.
$\therefore \angle CEF=180^{\circ}-x$，
$\therefore \angle CEH=\angle CEF+\angle FEH=180^{\circ}-x+30^{\circ}=210^{\circ}-x$.
$\because EQ$平分$\angle CEH$，
$\therefore \angle QEH=\frac{1}{2}\angle CEH=105^{\circ}-\frac{1}{2}x$.
$\because \angle Q+\angle QEH+\angle QPE=180^{\circ}$，
$\therefore 15^{\circ}+\frac{1}{2}x+105^{\circ}-\frac{1}{2}x+\angle QPE=180^{\circ}$，
$\therefore \angle QPE=60^{\circ}$.
$\because \angle H=60^{\circ}$，$\therefore \angle QPE=\angle H$，
$\therefore PQ// FH$.