《2025年全优标准卷八年级数学上册人教版》

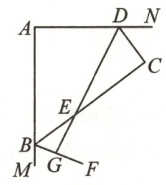
22. (10 分) 如图,在四边形 $ABCD$ 中,$\angle A = x^{\circ}$,$\angle C = y^{\circ}$,且 $0＜x＜180$,$0＜y＜180$.
(1) $\angle ABC+\angle ADC=$(360 - x - y)$^{\circ}$;(用含 $x$,$y$ 的代数式表示)
(2) 若 $x = y = 90$,$BF$ 平分与$\angle ABC$ 相邻的外角$\angle CBM$,$DG$ 平分$\angle ADC$ 交 $BC$ 于点 $E$、交 $BF$ 于点 $G$,试判断 $DG$ 与 $BF$ 的位置关系,并说明理由.

答案： 22.解:
(1)(360 - x - y)【解析】
∵在四边形ABCD中,∠A=x°,∠C=y°,
∴∠ABC+∠ADC=360°-∠A-∠C=(360 - x - y)°.
(2)DG⊥BF,理由如下:
∵∠ABC+∠CBM=180°,∠ABC+∠ADC=(360 - x - y)°=(360 - 90 - 90)°=180°,
∴∠CBM=∠ADC.
∵BF平分∠CBM,DG平分∠ADC,
∴$∠CBF=\frac{1}{2}∠CBM,∠CDE=\frac{1}{2}∠ADC, $
∴∠CBF=∠CDE.
∵∠BED=∠CBF+∠BGE=∠CDE+∠C,
∴∠BGE=∠C=90°,
∴DG⊥BF.

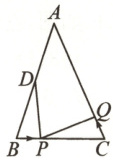
23. (10 分) 如图,在$\triangle ABC$ 中,$\angle B=\angle C$,$AB = AC = 6\,cm$,$BC = 4\,cm$,$D$ 为 $AB$ 的中点. 点 $P$ 在线段 $BC$ 上以 $1\,cm/s$ 的速度由点 $B$ 向点 $C$ 运动,同时,点 $Q$ 在线段 $CA$ 上由点 $C$ 向点 $A$ 运动.
(1) ①若点 $Q$ 的运动速度与点 $P$ 的运动速度相等,则经过几秒后,$\triangle BPD\cong\triangle CQP$? 请说明理由;
②若点 $Q$ 的运动速度与点 $P$ 的运动速度不相等,则当点 $Q$ 的运动速度为多少时,能够使$\triangle BPD$ 与$\triangle CQP$ 全等?
(2) 若点 $Q$ 以(1)②中的运动速度从点 $C$ 出发,点 $P$ 以 $1\,cm/s$ 的运动速度从点 $B$ 同时出发,都逆时针沿$\triangle ABC$ 的三边运动,则经过几秒后,点 $P$ 与点 $Q$ 第一次在$\triangle ABC$ 上相遇?

答案： 23.解:
(1)①经过1s后,△BPD≌△CQP,理由如下:
∵t = 1s,
∴BP = CQ = 1×1 = 1(cm).
∵AB = 6cm,D为AB的中点,
∴BD = 3cm.
∵PC = BC - BP,BC = 4cm,
∴PC = 4 - 1 = 3(cm),
∴PC = BD. 又∠B = ∠C,
∴△BPD≌△CQP. ②
∵v_P≠v_Q,
∴BP≠CQ,
∴BP与CQ不是对应边. 若△BPD≌△CPQ, 则BP = CP = 2cm,BD = CQ = 3cm,
∴点P、点Q运动的时间$t=\frac{BP}{1}=2s, $
∴$v_Q=\frac{CQ}{t}=\frac{3}{2}=1.5(cm/s); $若△BPD≌△PCQ,则BP = PC = 2cm, ∠DPB = ∠C,∠QPC = ∠B.
∵∠B = ∠C,
∴∠DPB = ∠B = ∠QPC = ∠C,
∴DB = DP = QP = QC = 3cm.
∵点P、点Q运动的时间$t=\frac{BP}{1}=2s, $
∴$v_Q=\frac{QC}{t}=\frac{3}{2}=1.5(cm/s); $若△BPD≌△PQC,则∠B = ∠QPC,BP = PQ.
∵∠B = ∠C,
∴∠QPC = ∠C,
∴PQ = CQ,
∴BP = CQ,与v_P≠v_Q矛盾，此情况舍去； 若△BPD≌△QPC,经检验，此情况不存在. 综上所述，当点Q的运动速度为1.5cm/s时，能够使△BPD与△CQP全等.
(2)设经过xs后，点P与点Q第一次相遇. 由题意,得1.5x = x + 2×6,解得x = 24,
∴经过24s后，点P与点Q第一次在△ABC上相遇.

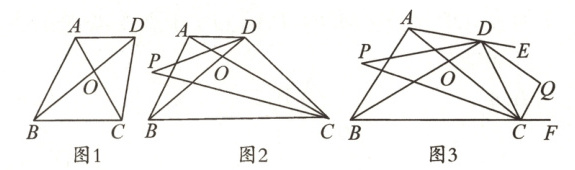
24. (13 分) 如图,在四边形 $ABCD$ 中,$AC$ 和 $BD$ 相交于点 $O$.
(1) 如图 1,若 $AD// BC$,$DB$ 平分$\angle ADC$,$\angle BCD = 100^{\circ}$,求$\angle DBC$ 的度数;
(2) 如图 2,若 $AD// BC$,$DP$ 平分$\angle ADB$,$CP$ 平分$\angle ACB$,求证:$\angle P=\frac{1}{2}\angle DOC$;
(3) 如图 3,若 $DP$ 平分$\angle ADB$,$CP$ 平分$\angle ACB$,$CQ$ 和 $DQ$ 分别是$\triangle BCD$ 和$\triangle ADC$ 的外角平分线,试探究$\angle P$,$\angle DOC$,$\angle Q$ 之间的数量关系.

答案：
24.解:
(1)
∵AD//BC,
∴∠ADC+∠BCD=180°. 又∠BCD=100°,
∴∠ADC=180°-∠BCD=80°.
∵DB平分∠ADC,
∴$∠ADB=\frac{1}{2}∠ADC=40°. $
∵AD//BC,
∴∠DBC=∠ADB=40°.
(2)证明:
∵DP平分∠ADB,
∴∠ADP=∠BDP.
∵CP平分∠ACB,
∴∠ACP=∠BCP. 设∠ADP=∠BDP=α,∠ACP=∠BCP=β, 则∠ADB=2α,∠ACB=2β.
∵AD//BC,
∴∠DBC=∠ADB=2α,
∴∠DOC=∠DBC+∠ACB=2α+2β. 如图,过点P作PE//AD,则∠DPE=∠ADP=α,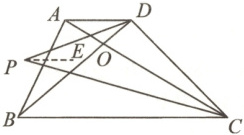
∵AD//BC,
∴PE//BC,
∴∠CPE=∠BCP=β,
∴∠DPC=∠DPE+∠CPE=α+β,
∴$∠DPC=\frac{1}{2}∠DOC. (3)$
∵DP平分∠ADB,CP平分∠ACB,CQ和DQ分别是△BCD和△ADC外角的平分线，
∴∠ADP=∠BDP,∠ACP=∠BCP, ∠EDQ=∠CDQ,∠DCQ=∠FCQ. 设∠ADP=∠BDP=x,∠ACP=∠BCP=y, ∠EDQ=∠CDQ=z,∠DCQ=∠FCQ=w, 则∠Q=180°-∠CDQ-∠DCQ=180°-z-w①, ∠ODC=180°-∠ADB-∠CDE=180°-2x-2z, ∠OCD=180°-∠ACB-∠DCF=180°-2y-2w,
∴∠DOC=180°-∠ODC-∠OCD=180°-(180°-2x-2z)-(180°-2y-2w)=2x+2y+2z+2w-180°②, ∠P=180°-∠BDP-∠ACP-∠ODC-∠OCD=180°-x-y-(180°-2x-2z)-(180°-2y-2w)=x+y+2z+2w-180°③, 由①×2-②+③×2=180°, 得2∠P+2∠Q-∠DOC=180°.