《2025年全优标准卷八年级数学上册人教版》

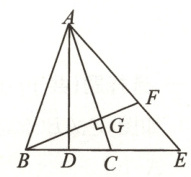
21. (8 分)如图,在等腰$\triangle ABC$中,$AB=AC$,AD 为中线,延长 DC 至点 E,使$∠E=∠DAE$,连接AE,过点 B 作 AC 的垂线,垂足为 G,交 AE 于点 F.
(1)若$∠BAC=40^{\circ }$,求$∠FBC$的度数;
(2)求证:$BF=AC$.

答案： 21.
(1)解：$\because AD$是中线,$\therefore BD=CD$.又$AB=AC$,
$AD=AD,\therefore \triangle ABD\cong\triangle ACD(SSS)$,
$\therefore \angle BAD=\angle CAD=\frac{1}{2}\angle BAC=20°$,
$\angle ABC=\angle ACB=\frac{180°-40°}{2}=70°$.
$\because BF\perp AC,\therefore \angle BGC=90°$,
$\therefore \angle FBC=90°-70°=20°$.
(2)证明：$\because \angle DAE=\angle E$,
$\angle BAF=\angle DAE+\angle BAD=\angle DAE+20°$,
$\angle AFB=\angle E+\angle CBF=\angle E+20°$,
$\therefore \angle BAF=\angle AFB$.
过点$B$作$BM\perp AF$于点$M$,则$\angle BMA=\angle BMF=90°$.
在$\triangle BMA$与$\triangle BMF$中,
$\begin{cases}\angle BAM=\angle BFM,\\\angle BMA=\angle BMF,\\BM=BM,\end{cases}$
$\therefore \triangle BMA\cong\triangle BMF(AAS),\therefore BA=BF$.
又$AB=AC,\therefore BF=AC$.

22. (9 分)如图,$\triangle ABC$的两边 AB,AC 上分别有两点 M,N,D 为$\triangle ABC$外一点,且$∠A=80^{\circ }$,$∠BDC=100^{\circ },∠MDN=50^{\circ },BD=DC$.
(1)猜想线段 MN,BM,NC 之间的数量关系并说明理由;
(2)若$AB=6,AC=7$,求$\triangle AMN$的周长.

答案：
22.解：
(1)$MN=BM+NC$,理由如下：
如图,延长$AB$,在$AB$的延长线上截取$BE=NC$,连接$DE$;

$\because$在$\triangle ABC$中,$\angle A=80°$,
$\therefore \angle ABC+\angle ACB=180°-80°=100°$.
$\because$在$\triangle BCD$中,$\angle BDC=100°$,
$\therefore \angle DBC+\angle DCB=180°-100°=80°$.
$\therefore \angle ABC+\angle ACB+\angle DBC+\angle DCB=180°$,
即$\angle ABD+\angle ACD=180°$.
$\because \angle DBE+\angle ABD=180°,\therefore \angle DBE=\angle ACD$.
在$\triangle DBE$和$\triangle DCN$中,$\begin{cases}BE=CN,\\\angle DBE=\angle DCN,\\DB=DC,\end{cases}$
$\therefore \triangle DBE\cong\triangle DCN(SAS)$,
$\therefore DE=DN,\angle EDB=\angle NDC$.
$\because \angle BDC=100°,\angle MDN=50°$,
$\therefore \angle BDM+\angle NDC=\angle BDC-\angle MDN=50°$,
$\therefore \angle MDE=\angle BDM+\angle EDB=\angle BDM+\angle NDC=50°,\therefore \angle MDE=\angle MDN=50°$.
在$\triangle MDE$和$\triangle MDN$中,$\begin{cases}DE=DN,\\\angle MDE=\angle MDN,\\DM=DM,\end{cases}$
$\therefore \triangle MDE\cong\triangle MDN(SAS),\therefore ME=MN$.
$\because ME=BM+BE=BM+NC$,
$\therefore MN=BM+NC$.
(2)由
(1)知$MN=BM+NC$,
$\therefore \triangle AMN$的周长是$AM+AN+MN=AM+AN+BM+NC=AB+AC=6+7=13$.

23. (10 分)【基础回顾】(1)如图 1,在$\triangle ABC$中,$∠BAC=90^{\circ },AB=AC$,直线 l 经过点 A,分别从点 B,C 向直线 l 作垂线,垂足分别为点 D,E. 求证:$\triangle ABD\cong \triangle CAE$;
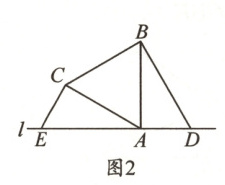
【变式探究】(2)如图 2,在$\triangle ABC$中,$AB=AC$,直线 l 经过点 A,点 D,E 分别在直线 l 上,如果$∠CEA=∠ADB=∠BAC$,试猜想 DE,BD,CE 之间有何数量关系,并给予证明;
【拓展应用】(3)小明在科技创新大赛上创作了一幅机器人图案,大致图形如图 3 所示,以$\triangle ABC$的边 AB,AC 为一边向外作$\triangle BAD$和$\triangle CAE$,其中$∠BAD=∠CAE=90^{\circ },AB=AD$,$AC=AE$,AG 是边 BC 上的高. 延长 GA 交 DE 于点 H,设$\triangle ADH$的面积为$S_{1}$,$\triangle AEH$的面积为$S_{2}$,试猜想$S_{1}$与$S_{2}$之间的大小关系并说明理由.

答案：
23.
(1)证明：$\because BD\perp$直线$l,CE\perp$直线$l$,
$\therefore \angle BDA=\angle AEC=90°$,
$\therefore \angle DAB+\angle DBA=90°$.
$\because \angle BAC=90°,\therefore \angle DAB+\angle EAC=90°$,
$\therefore \angle DBA=\angle EAC$.
在$\triangle ABD$和$\triangle CAE$中,$\begin{cases}\angle BDA=\angle AEC,\\\angle DBA=\angle EAC,\\AB=CA,\end{cases}$
$\therefore \triangle ABD\cong\triangle CAE(AAS)$.
(2)解：$DE=BD+CE$,证明如下：
$\because \angle EAB$是$\triangle ABD$的外角,
$\therefore \angle EAB=\angle ADB+\angle DBA$,
$\therefore \angle EAC+\angle BAC=\angle ADB+\angle DBA$.
$\because \angle ADB=\angle BAC,\therefore \angle EAC=\angle DBA$.
在$\triangle EAC$和$\triangle DBA$中,$\begin{cases}\angle EAC=\angle DBA,\\\angle CEA=\angle ADB,\\AB=CA,\end{cases}$
$\therefore \triangle EAC\cong\triangle DBA(AAS)$,
$\therefore CE=AD,AE=BD$,
$\therefore DE=AE+AD=BD+CE$.
(3)$S_1=S_2$,理由如下：
如图,过点$D$作$DM\perp AH$交$AH$的延长线于点$M$,过点$E$作$EN\perp AH$于点$N$,则$\angle M=\angle ANE=90°$.

$\because AG\perp BC,\therefore \angle AGB=\angle M$,
$\therefore \angle ABG+\angle BAG=90°$.
$\because \angle BAD=90°,\therefore \angle BAG+\angle DAM=90°$,
$\therefore \angle ABG=\angle DAM$.
在$\triangle ABG$和$\triangle DAM$中,$\begin{cases}\angle AGB=\angle M,\\\angle ABG=\angle DAM,\\AB=DA,\end{cases}$
$\therefore \triangle ABG\cong\triangle DAM(AAS),\therefore DM=AG$.
同理,可证得$\triangle AGC\cong\triangle ENA$,
$\therefore EN=AG,\therefore DM=EN$.
$\because S_1=\frac{1}{2}AH· DM,S_2=\frac{1}{2}AH· EN$,
$\therefore S_1=S_2$.

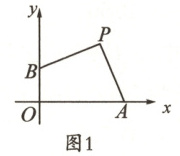
24. (10 分)如图,在平面直角坐标系中,$P(4,4)$,
(1)如图 1,当点 A 在 x 轴的正半轴上运动,点 B 在 y 轴的正半轴上运动($OA≠OB$),且$PA=PB$时,
①求证:$PA⊥PB$;
②求$OA+OB$的值;
(2)如图 2,当点 A 在 x 轴的正半轴上运动,点 B 在 y 轴的负半轴上运动,且$PA=PB$时,求$OA - OB$的值.

答案：
24.
(1)①证明：如图1,过点$P$作$PE\perp x$轴于点$E$, 作$PF\perp y$轴于点$F$,则$PE\perp PF$.

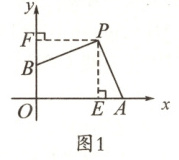
$\because P(4,4),\therefore PE=PF=4$. 在$\text{Rt}\triangle APE$和$\text{Rt}\triangle BPF$中,$\begin{cases}PA=PB,\\PE=PF,\end{cases}$ $\therefore \text{Rt}\triangle APE\cong\text{Rt}\triangle BPF(HL)$, $\therefore \angle APE=\angle BPF$, $\therefore \angle APB=\angle APE+\angle BPE=\angle BPF+\angle BPE=\angle EPF=90^\circ$, $\therefore PA\perp PB$.
②解：$\because \text{Rt}\triangle APE\cong\text{Rt}\triangle BPF,\therefore BF=AE$. $\because OA=OE+AE,OB=OF-BF$, $\therefore OA+OB=OE+AE+OF-BF=OE+OF=4+4=8$.
(2)解：如图2,过点$P$作$PM\perp x$轴于点$M$,作$PN\perp y$轴于点$N$.
 
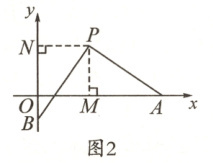
易证得$\text{Rt}\triangle APM\cong\text{Rt}\triangle BPN(HL)$, $\therefore AM=BN$. $\because OA=OM+AM=4+BN=4+ON+OB=8+OB$, $\therefore OA-OB=8+OB-OB=8$.