《2025年全优标准卷八年级数学上册人教版》

19. (7 分)阅读下列解题的过程.
分解因式:$x^{4}+64$.
解:$x^{4}+64 = x^{4}+16x^{2}+64 - 16x^{2}$
$=(x^{2}+8)^{2}-16x^{2}$
$=(x^{2}+8 + 4x)(x^{2}+8 - 4x)$.
请按照上述解题思路完成下列因式分解.
(1)$a^{4}+4$;
(2)$x^{4}-43x^{2}y^{2}+81y^{4}$.

答案： 19.解：
(1)原式$=a^4+4a^2+4-4a^2=(a^2+2)^2-4a^2=(a^2+2a+2)(a^2-2a+2).$
(2)原式$=x^4-18x^2y^2+81y^4-25x^2y^2=(x^2-9y^2)^2-25x^2y^2=(x^2-9y^2+5xy)(x^2-9y^2-5xy).$

$20. (9 $分$)$数学活动课上$,$张老师准备了若干张如图$ 1 $所示的三种纸片$,A $种纸片是边长为$a$的正方形$,B $种纸片是边长为$b$的正方形$,C $种纸片是长为$b,$宽为$a$的长方形$,$并用一张$ A $种纸片$,$一张$ B $种纸片$,$两张$ C $种纸片拼成了如图$ 2 $所示的大正方形$.$　　
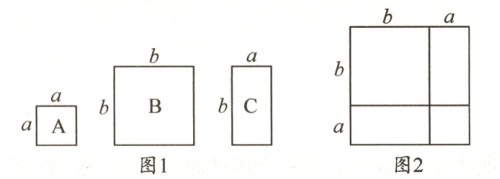
$(1)$观察图$ 2,$写出代数式$(a + b)^{2},a^{2}+b^{2},ab$之间的等量关系$:$　　$(a+b)^2=a^2+b^2+2ab$　　$;$　　
$(2)$根据$(1)$中的等量关系$,$解决下列问题$:$　　
$①$已知$a + b = 4,a^{2}+b^{2}=10,$求$ab$的值$;$　　
$②$已知$(x - 2026)^{2}+(x - 2024)^{2}=130,$求$x - 2025$的值$.$　　

答案： 20.解：$(1)(a+b)^2=a^2+b^2+2ab$
(2)①由
(1)知$2ab=(a+b)^2-(a^2+b^2)=4^2-10=16-10=6,$
∴ab=3.
②令x-2025=t,则$(t-1)^2+(t+1)^2=130，$
∴$t^2-2t+1+t^2+2t+1=130，$
∴$t^2=64,$
∴t=±8，
故x-2025=±8.

$21. (10 $分$)$下面是某同学对多项式$(x^{2}-2x)(x^{2}-2x + 2)+1$进行因式分解的过程$:$　　
解$:$设$x^{2}-2x = y,$　　
则原式$= y(y + 2)+1($第一步$)$　　
$= y^{2}+2y + 1($第二步$)$　　
$=(y + 1)^{2}($第三步$)$　　
$=(x^{2}-2x + 1)^{2}($第四步$).$　　
回答下列问题$:$　　
$(1)$该同学第二步到第三步运用了　　$C$　　$;$　　
$A. $提取公因式　　
$B. $平方差公式　　
$C. $完全平方公式　　
$(2)$该同学因式分解的结果是否彻底$?$　　不彻底　　$($填$“$彻底$”$或$“$不彻底$”),$若不彻底$,$则该因式分解的最终结果为　　$(x-1)^4$　　$;$　　
$(3)$请你模仿上述方法$,$对多项式$(x^{2}-2)(x^{2}-6)+4$进行因式分解$.$　　

答案： 21.解：
(1)C
(2)不彻底$(x-1)^4【$解析】该同学因式分解的结果不彻底，
∵$x^2-2x+1=(x-1)^2，$
∴该因式分解的最终结果为$(x-1)^4.$
(3)设$x^2-2=y，$
则原式$=y(y-4)+4=y^2-4y+4=(y-2)^2=(x^2-2-2)^2=(x^2-4)^2=(x-2)^2(x+2)^2.$