11. (12分)如图, 在 $ \triangle OAB $ 和 $ \triangle OCD $ 中, $ OA = OB $, $ OC = OD $, $ \angle AOB = \angle COD = \alpha $, $ AC $, $ BD $ 交于点 $ M $。
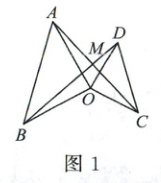

(1)如图1, 当 $ \alpha = 90° $ 时, $ \angle AMD $ 的度数为______。
(2)如图2, 当 $ \alpha = 60° $ 时, 求 $ \angle AMD $ 的度数。
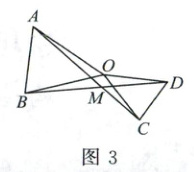
(3)如图3, 当 $ \triangle OCD $ 绕点 $ O $ 旋转任意角度时, $ \angle AMD $ 与 $ \alpha $ 是否存在着某种确定的数量关系? 若存在, 请你用 $ \alpha $ 表示 $ \angle AMD $, 并用图3进行说明; 若不存在, 请说明理由。



(1)如图1, 当 $ \alpha = 90° $ 时, $ \angle AMD $ 的度数为______。
(2)如图2, 当 $ \alpha = 60° $ 时, 求 $ \angle AMD $ 的度数。
(3)如图3, 当 $ \triangle OCD $ 绕点 $ O $ 旋转任意角度时, $ \angle AMD $ 与 $ \alpha $ 是否存在着某种确定的数量关系? 若存在, 请你用 $ \alpha $ 表示 $ \angle AMD $, 并用图3进行说明; 若不存在, 请说明理由。
答案:
(1)如图 1,设 OA 交 BD 于点 K。

因为∠AOB=∠COD=α,
所以∠BOD=∠AOC。
在△AOC 和△BOD 中,
OA=OB,
∠AOC=∠BOD,
OC=OD,
所以△AOC≌△BOD(SAS)。
所以∠OAC=∠OBD。
因为∠AKM=∠BKO,
所以∠AMK=∠BOK=90°。
所以∠AMD=180°-90°=90°。
故答案为 90°。
(2)如图 2,设 OA 交 BD 于点 K。

因为∠AOB=∠COD=α,
所以∠BOD=∠AOC。
在△AOC 和△BOD 中,
OA=OB,
∠AOC=∠BOD,
OC=OD,
所以△AOC≌△BOD(SAS)。
所以∠OAC=∠OBD。
因为∠AKM=∠BKO,
所以∠AMK=∠BOK=60°。
所以∠AMD=180°-60°=120°。
(3)存在。∠AMD=180°-α。
如图 3,设 AC 交 OB 于点 K。

因为∠AOB=∠COD=α,
所以∠BOD=∠AOC。
在△AOC 和△BOD 中,
OA=OB,
∠AOC=∠BOD,
OC=OD,
所以△AOC≌△BOD(SAS)。
所以∠OAC=∠OBD。
因为∠AKO=∠BKM,
所以∠BMK=∠AOK=α。
所以∠AMD=180°-α。
(1)如图 1,设 OA 交 BD 于点 K。

因为∠AOB=∠COD=α,
所以∠BOD=∠AOC。
在△AOC 和△BOD 中,
OA=OB,
∠AOC=∠BOD,
OC=OD,
所以△AOC≌△BOD(SAS)。
所以∠OAC=∠OBD。
因为∠AKM=∠BKO,
所以∠AMK=∠BOK=90°。
所以∠AMD=180°-90°=90°。
故答案为 90°。
(2)如图 2,设 OA 交 BD 于点 K。

因为∠AOB=∠COD=α,
所以∠BOD=∠AOC。
在△AOC 和△BOD 中,
OA=OB,
∠AOC=∠BOD,
OC=OD,
所以△AOC≌△BOD(SAS)。
所以∠OAC=∠OBD。
因为∠AKM=∠BKO,
所以∠AMK=∠BOK=60°。
所以∠AMD=180°-60°=120°。
(3)存在。∠AMD=180°-α。
如图 3,设 AC 交 OB 于点 K。

因为∠AOB=∠COD=α,
所以∠BOD=∠AOC。
在△AOC 和△BOD 中,
OA=OB,
∠AOC=∠BOD,
OC=OD,
所以△AOC≌△BOD(SAS)。
所以∠OAC=∠OBD。
因为∠AKO=∠BKM,
所以∠BMK=∠AOK=α。
所以∠AMD=180°-α。
查看更多完整答案,请扫码查看


