22. (10 分)(1)如图 1,分别以直角三角形的三边长为直径向外侧作半圆,则它们的面积 $ S_1 $,$ S_2 $,$ S_3 $ 之间满足的等量关系是 $\underline{
(2)如图 2,直角三角形的两条直角边长分别为 $ a $,$ b $,斜边长为 $ c $,分别以三边长为直径作半圆。若 $ a = 3 $,$ c = 5 $,求图中阴影部分的面积。

$S_1 + S_2 = S_3$
}$;(2)如图 2,直角三角形的两条直角边长分别为 $ a $,$ b $,斜边长为 $ c $,分别以三边长为直径作半圆。若 $ a = 3 $,$ c = 5 $,求图中阴影部分的面积。

(2)设以 $a$,$b$,$c$ 为直径的半圆的面积分别为 $S_1$,$S_2$,$S_3$,直角三角形的面积为 $S_4$。由(1)知 $S_1 + S_2 = S_3$。因为三角形是直角三角形,$a = 3$,$c = 5$,所以根据勾股定理,得 $b^2 = c^2 - a^2 = 5^2 - 3^2 = 16$。所以 $b = 4$。所以 $S_4 = \frac{1}{2}ab = \frac{1}{2} × 3 × 4 = 6$。所以阴影部分的面积为 $S_1 + S_2 + S_4 - S_3 = S_4 = 6$。
答案:
(1)$S_1 + S_2 = S_3$;
(2)设以 $a$,$b$,$c$ 为直径的半圆的面积分别为 $S_1$,$S_2$,$S_3$,直角三角形的面积为 $S_4$。由
(1)知 $S_1 + S_2 = S_3$。因为三角形是直角三角形,$a = 3$,$c = 5$,所以根据勾股定理,得 $b^2 = c^2 - a^2 = 5^2 - 3^2 = 16$。所以 $b = 4$。所以 $S_4 = \frac{1}{2}ab = \frac{1}{2} × 3 × 4 = 6$。所以阴影部分的面积为 $S_1 + S_2 + S_4 - S_3 = S_4 = 6$。
(1)$S_1 + S_2 = S_3$;
(2)设以 $a$,$b$,$c$ 为直径的半圆的面积分别为 $S_1$,$S_2$,$S_3$,直角三角形的面积为 $S_4$。由
(1)知 $S_1 + S_2 = S_3$。因为三角形是直角三角形,$a = 3$,$c = 5$,所以根据勾股定理,得 $b^2 = c^2 - a^2 = 5^2 - 3^2 = 16$。所以 $b = 4$。所以 $S_4 = \frac{1}{2}ab = \frac{1}{2} × 3 × 4 = 6$。所以阴影部分的面积为 $S_1 + S_2 + S_4 - S_3 = S_4 = 6$。
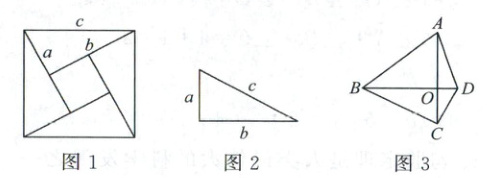
23. (12 分)[材料阅读]如图 1 是弦图的示意图,它由 4 个全等的直角三角形与 1 个小正方形组成,恰好拼成一个大正方形。大正方形的面积等于 $ c^2 $,同时它的面积又等于 4 个全等的直角三角形和小正方形的面积之和,于是有 $ 4 × \dfrac{1}{2}ab + (b - a)^2 = c^2 $,化简即得 $ a^2 + b^2 = c^2 $,这就验证了勾股定理。
[动手操作](1)请你利用 2 个或 4 个如图 2 所示的直角三角形设计出一个图形,画出来,并验证勾股定理;
[定理应用](2)如图 3,在四边形 $ ABCD $ 中,$ AC \perp BD $ 于点 $ O $,$ AB = 6 $,$ BC = 5 $,$ CD = 2 $,请求出 $ AD^2 $ 的值。

(1)
(2)
[动手操作](1)请你利用 2 个或 4 个如图 2 所示的直角三角形设计出一个图形,画出来,并验证勾股定理;
[定理应用](2)如图 3,在四边形 $ ABCD $ 中,$ AC \perp BD $ 于点 $ O $,$ AB = 6 $,$ BC = 5 $,$ CD = 2 $,请求出 $ AD^2 $ 的值。


(1)
(方案一)如图,当图形为直角梯形时,面积的两种求法如下:①$S_{梯形} = \frac{1}{2}(a + b)(a + b)$。②$S_{梯形} = \frac{1}{2}ab × 2 + \frac{1}{2}c^2$。所以 $\frac{1}{2}(a + b)(a + b) = \frac{1}{2}ab × 2 + \frac{1}{2}c^2$。整理,得 $a^2 + 2ab + b^2 = 2ab + c^2$,即 $a^2 + b^2 = c^2$。故勾股定理成立。(方案二)如图,当图形为大正方形时,面积的两种求法如下:①$S_{大正方形} = (a + b)^2$。②$S_{大正方形} = \frac{1}{2}ab × 4 + c^2$。所以 $(a + b)^2 = 2ab + c^2$,即 $a^2 + b^2 = c^2$。故勾股定理成立
(2)
由题意,得$\triangle ABO$,$\triangle BCO$,$\triangle CDO$,$\triangle ADO$ 均为直角三角形。由勾股定理,得 $AO^2 + BO^2 = AB^2$,$CO^2 + DO^2 = CD^2$,$AO^2 + DO^2 = AD^2$,$BO^2 + CO^2 = BC^2$,所以 $AO^2 + BO^2 + CO^2 + DO^2 = AB^2 + CD^2$,$AO^2 + BO^2 + CO^2 + DO^2 = AD^2 + BC^2$。所以 $AB^2 + CD^2 = AD^2 + BC^2$。所以 $6^2 + 2^2 = AD^2 + 5^2$。所以 $AD^2 = 15$
答案:
(1)(方案一)如图,当图形为直角梯形时,面积的两种求法如下:①$S_{梯形} = \frac{1}{2}(a + b)(a + b)$。②$S_{梯形} = \frac{1}{2}ab × 2 + \frac{1}{2}c^2$。所以 $\frac{1}{2}(a + b)(a + b) = \frac{1}{2}ab × 2 + \frac{1}{2}c^2$。整理,得 $a^2 + 2ab + b^2 = 2ab + c^2$,即 $a^2 + b^2 = c^2$。故勾股定理成立。(方案二)如图,当图形为大正方形时,面积的两种求法如下:①$S_{大正方形} = (a + b)^2$。②$S_{大正方形} = \frac{1}{2}ab × 4 + c^2$。所以 $(a + b)^2 = 2ab + c^2$,即 $a^2 + b^2 = c^2$。故勾股定理成立;
(2)由题意,得$\triangle ABO$,$\triangle BCO$,$\triangle CDO$,$\triangle ADO$ 均为直角三角形。由勾股定理,得 $AO^2 + BO^2 = AB^2$,$CO^2 + DO^2 = CD^2$,$AO^2 + DO^2 = AD^2$,$BO^2 + CO^2 = BC^2$,所以 $AO^2 + BO^2 + CO^2 + DO^2 = AB^2 + CD^2$,$AO^2 + BO^2 + CO^2 + DO^2 = AD^2 + BC^2$。所以 $AB^2 + CD^2 = AD^2 + BC^2$。所以 $6^2 + 2^2 = AD^2 + 5^2$。所以 $AD^2 = 15$。
(1)(方案一)如图,当图形为直角梯形时,面积的两种求法如下:①$S_{梯形} = \frac{1}{2}(a + b)(a + b)$。②$S_{梯形} = \frac{1}{2}ab × 2 + \frac{1}{2}c^2$。所以 $\frac{1}{2}(a + b)(a + b) = \frac{1}{2}ab × 2 + \frac{1}{2}c^2$。整理,得 $a^2 + 2ab + b^2 = 2ab + c^2$,即 $a^2 + b^2 = c^2$。故勾股定理成立。(方案二)如图,当图形为大正方形时,面积的两种求法如下:①$S_{大正方形} = (a + b)^2$。②$S_{大正方形} = \frac{1}{2}ab × 4 + c^2$。所以 $(a + b)^2 = 2ab + c^2$,即 $a^2 + b^2 = c^2$。故勾股定理成立;
(2)由题意,得$\triangle ABO$,$\triangle BCO$,$\triangle CDO$,$\triangle ADO$ 均为直角三角形。由勾股定理,得 $AO^2 + BO^2 = AB^2$,$CO^2 + DO^2 = CD^2$,$AO^2 + DO^2 = AD^2$,$BO^2 + CO^2 = BC^2$,所以 $AO^2 + BO^2 + CO^2 + DO^2 = AB^2 + CD^2$,$AO^2 + BO^2 + CO^2 + DO^2 = AD^2 + BC^2$。所以 $AB^2 + CD^2 = AD^2 + BC^2$。所以 $6^2 + 2^2 = AD^2 + 5^2$。所以 $AD^2 = 15$。
查看更多完整答案,请扫码查看


