1. 已知一个三角形的三边长分别为 $ a $,$ b $,$ c $,且它们满足 $ (a + b)^2 - c^2 = 2ab $,则该三角形的形状为(
A.锐角三角形
B.直角三角形
C.钝角三角形
D.无法确定
B
)A.锐角三角形
B.直角三角形
C.钝角三角形
D.无法确定
答案:
B
2. 如图是由两个直角三角形和三个正方形组成的图形,其中阴影部分的面积是(
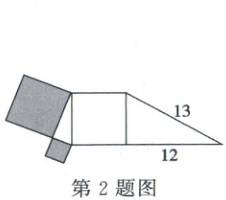
A.16
B.25
C.144
D.169
B
)
A.16
B.25
C.144
D.169
答案:
B
3. 如图,在 $ Rt\triangle ABC $ 中,$ \angle A = 90^{\circ} $,$ BD $ 平分 $ \angle ABC $,交 $ AC $ 于点 $ D $,且 $ AB = 4 $,$ BD = 5 $,则点 $ D $ 到 $ BC $ 的距离是(
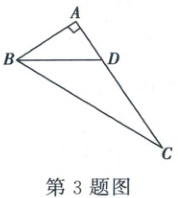
A.3
B.4
C.5
D.6
A
)
A.3
B.4
C.5
D.6
答案:
A
4. 满足下列条件的 $ \triangle ABC $,不是直角三角形的为(
A.$ \angle A = \angle B - \angle C $
B.$ \angle A : \angle B : \angle C = 1 : 1 : 2 $
C.$ b^2 = a^2 - c^2 $
D.$ a : b : c = 2 : 3 : 4 $
D
)A.$ \angle A = \angle B - \angle C $
B.$ \angle A : \angle B : \angle C = 1 : 1 : 2 $
C.$ b^2 = a^2 - c^2 $
D.$ a : b : c = 2 : 3 : 4 $
答案:
D
5. 勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载。如图 1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图 2 的方式放置在最大的正方形内。若知道图中阴影部分的面积,则一定能求出(
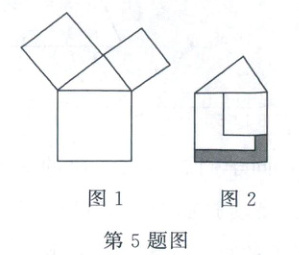
A.直角三角形的面积
B.最大的正方形的面积
C.较小的两个正方形重叠部分的面积
D.最大的正方形与直角三角形的面积和
C
)
A.直角三角形的面积
B.最大的正方形的面积
C.较小的两个正方形重叠部分的面积
D.最大的正方形与直角三角形的面积和
答案:
C
查看更多完整答案,请扫码查看


