11. (4分)如图, 将长方形$ABCD沿对角线BD$折叠, 使点$C落在点F$处, $BF交AD于点E$。若$∠BDC = 62^{\circ}$, 则$∠DEF$的度数为 (
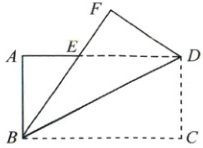
A.$31^{\circ}$
B.$28^{\circ}$
C.$62^{\circ}$
D.$56^{\circ}$
D
)
A.$31^{\circ}$
B.$28^{\circ}$
C.$62^{\circ}$
D.$56^{\circ}$
答案:
D
12. (4分)如图, 在$△ABC$中, $∠BAC > 90^{\circ}$, $D为BC$的中点, $E是AC$上一点, 将$△CDE沿DE$折叠, 使得点$C恰好落在BA延长线上的点F$处, 连接$AD$, $CF$, 则图中所有的等腰三角形的个数为 (
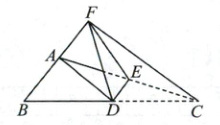
A.1个
B.2个
C.3个
D.4个
D
)
A.1个
B.2个
C.3个
D.4个
答案:
D
13. (4分)如图, 将$△ABC沿直线DE$折叠后, 使得点$B与点A$重合。已知$AC = 5\ cm$, $△ADC的周长为17\ cm$, 则$BC$的长为 (
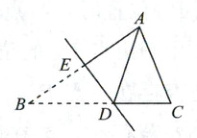
A.$7\ cm$
B.$10\ cm$
C.$12\ cm$
D.$22\ cm$
C
)
A.$7\ cm$
B.$10\ cm$
C.$12\ cm$
D.$22\ cm$
答案:
C
14. (4分)将一个长方形纸片按如图所示折叠, 若$∠1 = 40^{\circ}$, 则$∠2$的度数是 (
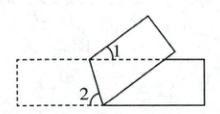
A.$40^{\circ}$
B.$50^{\circ}$
C.$60^{\circ}$
D.$70^{\circ}$
D
)
A.$40^{\circ}$
B.$50^{\circ}$
C.$60^{\circ}$
D.$70^{\circ}$
答案:
D
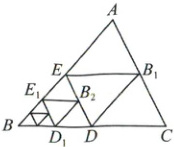
15. (4分)如图, 将$△ABC沿着过BC的中点D$的直线折叠, 使点$B落在边AC上的B_1$处, 称为第一次操作, 折痕$DE到AC的距离记为h_1$; 还原纸片后, 再将$△BDE沿着过BD的中点D_1$的直线折叠, 使点$B落在边DE上的B_2$处, 称为第二次操作, 折痕$D_1E_1到AC的距离记为h_2$; 按上述方法不断操作下去……经过第$n次操作后得到折痕D_{n - 1}E_{n - 1}$, 到$AC的距离记为h_n$。若$h_1 = 1$, 则$h_n$的值为 (
A.$1 + \frac{1}{2^{n - 1}}$
B.$1 + \frac{1}{2^n}$
C.$2 - \frac{1}{2^{n - 1}}$
D.$2 - \frac{1}{2^n}$
C
)
A.$1 + \frac{1}{2^{n - 1}}$
B.$1 + \frac{1}{2^n}$
C.$2 - \frac{1}{2^{n - 1}}$
D.$2 - \frac{1}{2^n}$
答案:
C
查看更多完整答案,请扫码查看


