《2025年同步练习册分层卷七年级数学上册鲁教版》

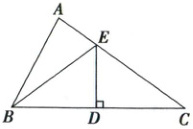
20. (10 分)如图,在△ABC 中,AB ＜ AC,边 BC 的垂直平分线 DE 交 BC 于点 D,交 AC 于点 E,AC = 8,△ABE 的周长为 14,求 AB 的长。

答案： 解：因为DE是边BC的垂直平分线，所以BE=CE。所以△ABE的周长=AB+AE+BE=AB+AE+CE=AB+AC。因为AC=8，△ABE的周长为14，所以AB+8=14。所以AB=6。

21. (10 分)数学课上,张老师讲解了下面的例题：
例 1 在等腰三角形 ABC 中,∠A = 110°,求∠B 的度数。(答案：35°)
例 2 在等腰三角形 ABC 中,∠A = 40°,求∠B 的度数。(答案：40°或 70°或 100°)
张老师启发同学们进行变式,小敏编了如下一题：
变式 在等腰三角形 ABC 中,∠A = 80°,求∠B 的度数。
(1)请解答以上的变式题；
(2)解(1)后,小敏发现,∠A 的度数不同,得到∠B 的度数的个数也可能不同。如果在等腰三角形 ABC 中,设∠A = x°,当∠B 有 3 个不同的度数时,请探索 x 的取值范围。

答案： 解：
(1)若∠A为顶角，则∠B=(180°-∠A)÷2=50°。若∠A为底角，∠B为顶角，则∠B=180°-2×80°=20°。若∠A为底角，∠B为底角，则∠B=80°。故∠B的度数为50°或20°或80°。
(2)分两种情况：①当90≤x＜180时，∠A只能为顶角，所以∠B的度数只有1个。②当0＜x＜90时，若∠A为顶角，则∠B=(180 - x)/2°。若∠A为底角，∠B为顶角，则∠B=(180 - 2x)°。若∠A为底角，∠B为底角，则∠B=x°。当(180 - x)/2≠180 - 2x且180 - 2x≠x且(180 - x)/2≠x，即x≠60时，∠B有3个不同的度数。综上所述，当0＜x＜90且x≠60时，∠B有3个不同的度数。