23. (12分)如图,在△ABC中,∠ACB= 90°,AC= CB,直线m过点C,分别过点A,B作直线m的垂线段,垂足分别为点D,E。
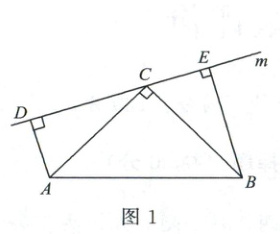
(1)如图1,当点A,B在直线m的同侧时,
①试说明:△ACD≌△CBE;
②直接写出线段DE,AD,BE之间的数量关系。
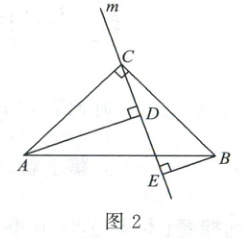
(2)如图2,当点A,B在直线m的异侧时,请问(1)中线段DE,AD,BE之间的数量关系还成立吗?若成立,请说明理由;若不成立,请给出正确的结论,并说明理由。


(1)如图1,当点A,B在直线m的同侧时,
①试说明:△ACD≌△CBE;
②直接写出线段DE,AD,BE之间的数量关系。
(2)如图2,当点A,B在直线m的异侧时,请问(1)中线段DE,AD,BE之间的数量关系还成立吗?若成立,请说明理由;若不成立,请给出正确的结论,并说明理由。
答案:
解:
(1)①因为 AD⊥m,BE⊥m,
所以∠ADC = ∠CEB = 90°。
所以∠ACD + ∠CAD = 90°。
又因为∠ACB = 90°,
所以∠ACD + ∠BCE = 180° - ∠ACB = 90°。
所以∠CAD = ∠BCE。
在△ACD 和△CBE 中,
∠CAD = ∠BCE,
∠ADC = ∠CEB,
AC = CB,
所以△ACD≌△CBE(AAS)。
②DE = AD + BE。
(2)
(1)中的数量关系不成立,正确的结论是:DE = AD - BE。理由如下:
因为 AD⊥m,BE⊥m,
所以∠ADC = ∠CEB = 90°。
所以∠ACD + ∠CAD = 90°。
又因为∠ACB = 90°,
即∠ACD + ∠BCE = 90°,
所以∠CAD = ∠BCE。
在△ACD 和△CBE 中,
∠CAD = ∠BCE,
∠ADC = ∠CEB,
AC = CB,
所以△ACD≌△CBE(AAS)。
所以 AD = CE,CD = BE。
所以 DE = CE - CD = AD - BE。
(1)①因为 AD⊥m,BE⊥m,
所以∠ADC = ∠CEB = 90°。
所以∠ACD + ∠CAD = 90°。
又因为∠ACB = 90°,
所以∠ACD + ∠BCE = 180° - ∠ACB = 90°。
所以∠CAD = ∠BCE。
在△ACD 和△CBE 中,
∠CAD = ∠BCE,
∠ADC = ∠CEB,
AC = CB,
所以△ACD≌△CBE(AAS)。
②DE = AD + BE。
(2)
(1)中的数量关系不成立,正确的结论是:DE = AD - BE。理由如下:
因为 AD⊥m,BE⊥m,
所以∠ADC = ∠CEB = 90°。
所以∠ACD + ∠CAD = 90°。
又因为∠ACB = 90°,
即∠ACD + ∠BCE = 90°,
所以∠CAD = ∠BCE。
在△ACD 和△CBE 中,
∠CAD = ∠BCE,
∠ADC = ∠CEB,
AC = CB,
所以△ACD≌△CBE(AAS)。
所以 AD = CE,CD = BE。
所以 DE = CE - CD = AD - BE。
查看更多完整答案,请扫码查看


