1. (8分)如图, $ \angle BAC = 90° $, $ AB = AC $, $ BD $ 是 $ \angle ABC $ 的平分线, 且 $ CE \perp BD $, 交 $ BD $ 的延长线于点 $ E $。试说明: $ BD = 2CE $。


答案:
解:如图,延长 CE 与 BA 的延长线相交于点 F。
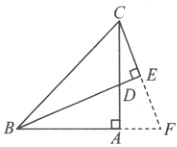
因为 CE⊥BE,∠BAC=90°,
所以∠ABD+∠F=90°,∠ACF+∠F=90°。
所以∠ABD=∠ACF。
在△ABD 和△ACF 中,
∠ABD=∠ACF,
AB=AC,
∠BAD=∠CAF,
所以△ABD≌△ACF(ASA)。
所以 BD=CF。
因为 BD 是∠ABC 的平分线,
所以∠EBC=∠EBF。
在△BCE 和△BFE 中,
∠EBC=∠EBF,
BE=BE,
∠CEB=∠FEB,
所以△BCE≌△BFE(ASA)。
所以 CE=EF。
所以 CF=2CE。
所以 BD=CF=2CE。
解:如图,延长 CE 与 BA 的延长线相交于点 F。

因为 CE⊥BE,∠BAC=90°,
所以∠ABD+∠F=90°,∠ACF+∠F=90°。
所以∠ABD=∠ACF。
在△ABD 和△ACF 中,
∠ABD=∠ACF,
AB=AC,
∠BAD=∠CAF,
所以△ABD≌△ACF(ASA)。
所以 BD=CF。
因为 BD 是∠ABC 的平分线,
所以∠EBC=∠EBF。
在△BCE 和△BFE 中,
∠EBC=∠EBF,
BE=BE,
∠CEB=∠FEB,
所以△BCE≌△BFE(ASA)。
所以 CE=EF。
所以 CF=2CE。
所以 BD=CF=2CE。
2. (8分)如图, $ \triangle ABC $ 为等边三角形, 延长 $ BC $ 到点 $ D $, 延长 $ BA $ 到点 $ E $, 使 $ AE = BD $, 连接 $ EC $, $ ED $。试说明: $ CE = DE $。


答案:
解:如图,延长 BD 至点 F,使 DF=BC,连接 EF。

因为 AE=BD,△ABC 为等边三角形,
所以 DF=BC=AB,∠B=60°。
所以 AE+AB=BD+DF,即 BE=BF。
所以△BEF 为等边三角形。
所以∠F=60°,BE=EF。
在△ECB 和△EDF 中,
BE=FE,
∠B=∠F,
BC=FD,
所以△ECB≌△EDF(SAS)。
所以 CE=DE。
解:如图,延长 BD 至点 F,使 DF=BC,连接 EF。

因为 AE=BD,△ABC 为等边三角形,
所以 DF=BC=AB,∠B=60°。
所以 AE+AB=BD+DF,即 BE=BF。
所以△BEF 为等边三角形。
所以∠F=60°,BE=EF。
在△ECB 和△EDF 中,
BE=FE,
∠B=∠F,
BC=FD,
所以△ECB≌△EDF(SAS)。
所以 CE=DE。
查看更多完整答案,请扫码查看


