《2025年同步练习册分层卷七年级数学上册鲁教版》

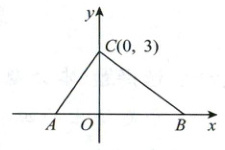
22. (10 分)如图,在平面直角坐标系中,点 $A$,$B$ 的坐标分别为 $A(a,0)$,$B(b,0)$,且 $a$,$b$ 满足 $|a + 2|+\sqrt{b - 4}= 0$,点 $C$ 的坐标为 $(0,3)$。
(1)求 $a$,$b$ 的值及 $S_{\triangle ABC}$；
(2)若点 $M$ 在 $x$ 轴上,且 $S_{\triangle ACM}= \frac{1}{3}S_{\triangle ABC}$,求点 $M$ 的坐标。

答案： 解：
(1)因为|a + 2|+$\sqrt{b - 4}$= 0，所以a+2=0，b-4=0。所以a=-2，b=4。所以A(-2，0)，B(4，0)。又因为C(0，3)，所以AB=|-2-4|=6，CO=3。所以S△ABC= $\frac{1}{2}$AB·CO= $\frac{1}{2}$×6×3=9。
(2)若点M在x轴上，且S△ACM= $\frac{1}{3}$S△ABC，求点M的坐标。设点M的坐标为(x，0)，则AM=|x-(-2)|=|x+2|。因为S△ACM= $\frac{1}{3}$S△ABC，所以 $\frac{1}{2}$AM·CO= $\frac{1}{3}$×9，即 $\frac{1}{2}$|x+2|×3=3。所以|x+2|=2，即x+2=±2，解得x=0或x=-4。故点M的坐标为(0，0)或(-4，0)。

23. (12 分)在平面直角坐标系中,已知 $A(x_1,y_1)$,$B(x_2,y_2)$。若 $x_2 - x_1 = y_2 - y_1 \neq 0$,则称点 $A$ 与点 $B$ 互为“对角点”。例如,$A(-1,3)$,$B(2,6)$,因为 $2 - (-1)= 6 - 3 \neq 0$,所以点 $A$ 与点 $B$ 互为“对角点”。
(1)若点 $A$ 的坐标是 $(4,-2)$,则在点 $B_1(2,0)$,$B_2(-1,-7)$,$B_3(0,-6)$ 中,点 $A$ 的“对角点”为 $B_2(-1,-7)$，$B_3(0,-6)$；
(2)若点 $A(-2,4)$ 的“对角点”$B$ 在坐标轴上,求点 $B$ 的坐标。
解：①当点B在x轴上时，设B(t，0)。由题意，得t-(-2)=0-4，解得t=-6。所以B(-6，0)。②当点B在y轴上时，设B(0，b)。由题意，得0-(-2)=b-4，解得b=6。所以B(0，6)。综上所述，点A(-2，4)的“对角点”B的坐标为(-6，0)或(0，6)。

答案： 解：
(1)B₂(-1，-7)，B₃(0，-6)
(2)若点A(-2，4)的“对角点”B在坐标轴上，求点B的坐标。①当点B在x轴上时，设B(t，0)。由题意，得t-(-2)=0-4，解得t=-6。所以B(-6，0)。②当点B在y轴上时，设B(0，b)。由题意，得0-(-2)=b-4，解得b=6。所以B(0，6)。综上所述，点A(-2，4)的“对角点”B的坐标为(-6，0)或(0，6)。