《2025年状元成才路创优作业100分五年级数学上册人教版湖南专版》

1. 省略乘号写出下面各式。
$6×k=$6k $n×1=$n
$y×2025=$2025y $1×h×4=$4h
$a×2=$2a $m\cdot m=$$m^{2}$
$x×6×y=$6xy $9×b×b=$$9b^{2}$

答案： 6k n 2025y 4h 2a $m^{2}$ 6xy $9b^{2}$

2. 根据运算律在$□$里填上适当的数或字母。
(1)$a + 12 + b = □ + □ + 12$
(2)$7\cdot (a + b) = 7\cdot □ + 7\cdot □$
(3)$55m + 45m = □\cdot (□ + □)$
(4)$(a\cdot b)\cdot 125 = a\cdot (□\cdot □)$
(5)$76×m + n×□ = (□ + □)×76$
(6)$n÷1.25÷□ = □÷(1.25×8)$

(1)$a + 12 + b = a + b + 12$
(2)$7\cdot (a + b) = 7\cdot a + 7\cdot b$
(3)$55m + 45m = m\cdot (55 + 45)$
(4)$(a\cdot b)\cdot 125 = a\cdot (b\cdot 125)$
(5)$76×m + n×76 = (m + n)×76$
(6)$n÷1.25÷8 = n÷(1.25×8)$

答案：
(1)ab
(2)a b
(3)m 55 45
(4)b 125
(5)76 mn
(6)8 n

3. 短道速滑是冬季奥运会项目,赛程全长$s\ m$,某运动员滑完全程需要$t$秒,每秒滑行$v\ m$。
(1)分别用字母表示$s$、$v和t$之间的数量关系。
$s = $vt
$v = $s÷ t
$t = $s÷ v
(2)当$s = 500$,$t = 42$时,$v ≈$(11.90)。(得数保留两位小数)

答案：
(1)vt $s÷ t$ $s÷ v$
(2)11.90

4. 张叔叔在大棚里收获了一些水培生菜,打算拿到菜市场去卖。

如果每千克水培生菜卖$19.8$元,那么张叔叔卖多少千克的水培生菜可以收入$1386$元?(先将表格填完整,再根据表中的公式解决问题)
7x
240÷ y
c÷ a
m=c÷ a=1386÷19.8=70

答案： (表格从上往下)7x $240÷ y$ $c÷ a$ $m=c÷ a=1386÷19.8=70$

5. 如图所示,甲是正方形,乙是长方形。
(1)右边整个图形的周长用字母表示是(4a+2b),面积用字母表示是(a²+ab)。
(2)如果$a = 5\ cm$,$b = 14\ cm$,整个图形的周长和面积分别是多少?
周长:$4a+2b=4×5+2×14=48(cm)$ 面积:$a²+ab=5×5+14×5=95(cm²)$

答案：
(1)$4a+2b$ $a^{2}+ab$
(2)周长:$4a+2b=4×5+2×14=48(cm)$ 面积:$a^{2}+ab=5×5+14×5=95(cm^{2})$

6. 菲菲有一张长$a\ cm$、宽$b\ cm$的长方形纸,如图所示($a ＞ b$)。她从中剪下了一个最大的正方形。

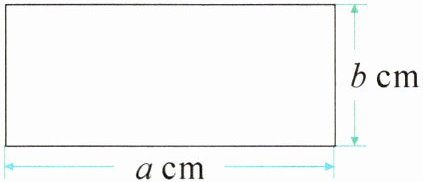
(1)剪下的正方形纸的周长是(4b)$cm$,面积是($b^{2}$)$cm^{2}$。
(2)剩下图形的周长是(2a)$cm$,面积是($ab - b^{2}$)$cm^{2}$。
(3)如果她剪下的正方形纸的周长是$28\ cm$,剩下的图形也是一个正方形,那么原长方形纸的长是(14)$cm$,宽是(7)$cm$。

答案：
(1)4b $b^{2}$
(2)2a $ab - b^{2}$
(3)14 7