1. 扇形统计图中,所有扇形的百分比之和应该(
A.小于1
B.等于1
C.大于1
D.等于100
B
)。A.小于1
B.等于1
C.大于1
D.等于100
答案:
解析:扇形统计图是用整个圆表示总数,用圆内各个扇形的大小表示各部分数量占总数的百分数。通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系。因为整个圆代表总数,即$100\%$或$1$,所以所有扇形的百分比之和应该等于$1$或$100\%$。但在数学表述上,我们通常说等于$1$来表示整体,而在实际应用中可能会说等于$100\%$。但根据题目选项,这里问的是数学上的表述。
答案:B
答案:B
2. 为了反映空气中的主要成分所占的体积和总体积的关系,选用(
A.条形
B.折线
C.扇形
D.复式条形
C
)统计图比较合适。A.条形
B.折线
C.扇形
D.复式条形
答案:
解析:
本题考查的是统计图的认识及应用。我们需要分析各种统计图的特点,并根据题目要求选择合适的统计图。
A选项条形图:主要用于看出数量的多少,便于比较几组数据的大小,不能反映部分与整体的关系。
B选项折线图:主要用于看出数量的变化趋势,也不能反映部分与整体的关系。
C选项扇形图:主要用于反映各部分占整体的百分比,即部分与整体的关系,能很好地反映空气中的主要成分所占的体积和总体积的关系。
D选项复式条形图:用于比较多个分类数据的数量大小,同样不能反映部分与整体的关系。
根据以上分析,为了反映空气中的主要成分所占的体积和总体积的关系,选用扇形统计图最合适。
答案:C
本题考查的是统计图的认识及应用。我们需要分析各种统计图的特点,并根据题目要求选择合适的统计图。
A选项条形图:主要用于看出数量的多少,便于比较几组数据的大小,不能反映部分与整体的关系。
B选项折线图:主要用于看出数量的变化趋势,也不能反映部分与整体的关系。
C选项扇形图:主要用于反映各部分占整体的百分比,即部分与整体的关系,能很好地反映空气中的主要成分所占的体积和总体积的关系。
D选项复式条形图:用于比较多个分类数据的数量大小,同样不能反映部分与整体的关系。
根据以上分析,为了反映空气中的主要成分所占的体积和总体积的关系,选用扇形统计图最合适。
答案:C
3. 小青第一节课到四楼上数学课,第二节课到二楼上艺术课,第三节课到三楼上课学课,中午到一楼食堂吃饭。下面能比较准确地描述这一过程的是图(
B
)。
答案:
解析:
分析题目可知,小青的行动轨迹在楼层间上下移动,且每个楼层停留的时间不确定,但上下楼层的时间点是可以确定的。
第一节课:小青从起始楼层(假设为1楼)上到4楼。
第二节课:从4楼下到2楼。
第三节课:从2楼上到3楼。
中午:从3楼下到1楼。
现在,根据这个轨迹来分析选项:
A选项:图中显示从起始楼层上到4楼,然后直接下到比2楼还低的楼层(可能是1楼,但紧接着又上升,不符合第二节课后下到2楼的情况),此选项不符合。
B选项:图中显示从起始楼层上到4楼,然后下到2楼,再上到3楼,最后下到1楼,符合。
C选项:图中显示楼层变化与小青的实际行动不符,特别是在第二节课后和第三节课前的变化,此选项不符合。
D选项:图中显示楼层变化也不符合小青的实际行动,特别是在从4楼下到2楼之后的变化,此选项不符合。
所以只有B选项符合小青的行动轨迹。
答案:B
分析题目可知,小青的行动轨迹在楼层间上下移动,且每个楼层停留的时间不确定,但上下楼层的时间点是可以确定的。
第一节课:小青从起始楼层(假设为1楼)上到4楼。
第二节课:从4楼下到2楼。
第三节课:从2楼上到3楼。
中午:从3楼下到1楼。
现在,根据这个轨迹来分析选项:
A选项:图中显示从起始楼层上到4楼,然后直接下到比2楼还低的楼层(可能是1楼,但紧接着又上升,不符合第二节课后下到2楼的情况),此选项不符合。
B选项:图中显示从起始楼层上到4楼,然后下到2楼,再上到3楼,最后下到1楼,符合。
C选项:图中显示楼层变化与小青的实际行动不符,特别是在第二节课后和第三节课前的变化,此选项不符合。
D选项:图中显示楼层变化也不符合小青的实际行动,特别是在从4楼下到2楼之后的变化,此选项不符合。
所以只有B选项符合小青的行动轨迹。
答案:B
4. 古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,把1,4,9,16…这样的数称为“正方形数”。从下右图中可以看出,任何一个大于1的“正方形数”都可以看作是两个相邻的“三角形数”之和。下列算式中,符合这一规律的是(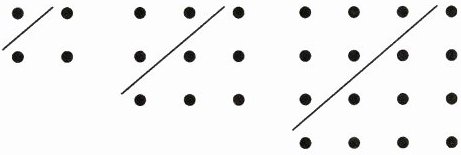
A.13= 3+10
B.25= 9+16
C.36= 15+21
D.49= 18+31
C
)。
A.13= 3+10
B.25= 9+16
C.36= 15+21
D.49= 18+31
答案:
解析:
三角形数:这些数可以表示成$1, 3, 6, 10, \cdots$,可以观察到第$n$个三角形数是前$n$个自然数之和,即第$n$个三角形数为$\frac{n(n+1)}{2}$。
正方形数:这些数可以表示成$1, 4, 9, 16, \cdots$,即第$n$个正方形数为$n^2$。
根据题意,任何一个大于1的正方形数都可以看作是两个相邻三角形数之和。
A选项:$13 = 3 + 10$,
$3$不是正方形数,所以A选项不符合条件。
B选项:$25 = 9 + 16$,
$9$和$16$都是正方形数,而不是三角形数,所以B选项不符合条件。
C选项:$36 = 15 + 21$,
第$5$个三角形数为$\frac{5 × (5+1)}{2} = 15$,
第$6$个三角形数为$\frac{6 × (6+1)}{2} = 21$,
$15 + 21 = 36$,
所以C选项符合条件。
D选项:$49 = 18 + 31$,
第$6$个三角形数为$21$,第$7$个三角形数为$28$,
$18$和$31$都不是三角形数,所以D选项不符合条件。
答案:C.$36 = 15 + 21$。
三角形数:这些数可以表示成$1, 3, 6, 10, \cdots$,可以观察到第$n$个三角形数是前$n$个自然数之和,即第$n$个三角形数为$\frac{n(n+1)}{2}$。
正方形数:这些数可以表示成$1, 4, 9, 16, \cdots$,即第$n$个正方形数为$n^2$。
根据题意,任何一个大于1的正方形数都可以看作是两个相邻三角形数之和。
A选项:$13 = 3 + 10$,
$3$不是正方形数,所以A选项不符合条件。
B选项:$25 = 9 + 16$,
$9$和$16$都是正方形数,而不是三角形数,所以B选项不符合条件。
C选项:$36 = 15 + 21$,
第$5$个三角形数为$\frac{5 × (5+1)}{2} = 15$,
第$6$个三角形数为$\frac{6 × (6+1)}{2} = 21$,
$15 + 21 = 36$,
所以C选项符合条件。
D选项:$49 = 18 + 31$,
第$6$个三角形数为$21$,第$7$个三角形数为$28$,
$18$和$31$都不是三角形数,所以D选项不符合条件。
答案:C.$36 = 15 + 21$。
5. 5名同学在公园相遇,见面时握手致意,已知A同学握了1次手,B同学握了4次手,C同学握了2次手,D同学握了3次手。到目前为止,E同学握了(
A.1
B.2
C.3
D.4
B
)次手。A.1
B.2
C.3
D.4
答案:
解析:
这是一个关于握手次数的问题,可以通过分析每个人握手的次数来推断出E同学握手的次数。
首先,我们知道A同学握了1次手,这意味着他只和一个人握了手。
因为B同学握了4次手,他必然和除了自己之外的其他四名同学都握了手,包括A同学。
所以A同学唯一的一次握手是和B同学。
接下来,D同学握了3次手,由于A同学只和B同学握了手,所以D同学没有和A同学握手,而是和B,C,E同学握了手。
C同学握了2次手,由于他已经和B同学握过手,且D同学也和他握了手,所以C同学的两次握手是和B同学与D同学。
最后,来看E同学,他已经和B同学与D同学握了手,由于A同学只和B同学握了手,C同学只和B,D同学握了手。
所以E同学握手的次数就是除了和B,D同学握手之外,没有和其他人握手,因此E同学握了2次手。
答案:B.2。
这是一个关于握手次数的问题,可以通过分析每个人握手的次数来推断出E同学握手的次数。
首先,我们知道A同学握了1次手,这意味着他只和一个人握了手。
因为B同学握了4次手,他必然和除了自己之外的其他四名同学都握了手,包括A同学。
所以A同学唯一的一次握手是和B同学。
接下来,D同学握了3次手,由于A同学只和B同学握了手,所以D同学没有和A同学握手,而是和B,C,E同学握了手。
C同学握了2次手,由于他已经和B同学握过手,且D同学也和他握了手,所以C同学的两次握手是和B同学与D同学。
最后,来看E同学,他已经和B同学与D同学握了手,由于A同学只和B同学握了手,C同学只和B,D同学握了手。
所以E同学握手的次数就是除了和B,D同学握手之外,没有和其他人握手,因此E同学握了2次手。
答案:B.2。
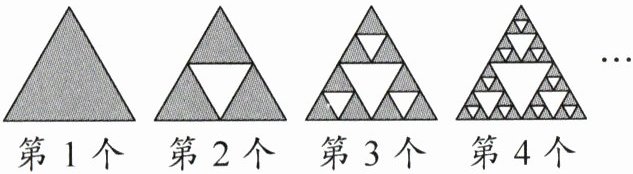
6. 观察下右图中每个大三角形中白色三角形的排列规律,第5个大三角形中有(
A.13
B.40
C.121
D.484
B
)个白色三角形。...
A.13
B.40
C.121
D.484
答案:
第1个:0个
第2个:1个
第3个:1+3=4个
第4个:4+9=13个
第5个:13+27=40个
答案:B
第2个:1个
第3个:1+3=4个
第4个:4+9=13个
第5个:13+27=40个
答案:B
1. 已知$2+4= 2×3= 6$,$2+4+6= 3×4= 12$,$2+4+6+8= 4×5= 20$,…,则$2+4+6+8+…+200= (
100
)×(101
)= (10100
)$。(3分)
答案:
观察可知:算式左边是连续偶数的和,第一个算式有2个加数,结果为2×3;第二个算式有3个加数,结果为3×4;第三个算式有4个加数,结果为4×5。
算式中最后一个数为200,因为每个加数都是2的倍数,所以加数的个数为200÷2 = 100个。
则结果为100×(100 + 1) = 100×101 = 10100。
100;101;10100
算式中最后一个数为200,因为每个加数都是2的倍数,所以加数的个数为200÷2 = 100个。
则结果为100×(100 + 1) = 100×101 = 10100。
100;101;10100
查看更多完整答案,请扫码查看


