1. 一个比的比值是$\frac{3}{7}$,如果后项乘$\frac{1}{2}$,前项不变,那么现在的比值是(
A.$\frac{6}{7}$
B.$\frac{3}{14}$
C.$\frac{7}{6}$
D.$\frac{14}{3}$
A
)。A.$\frac{6}{7}$
B.$\frac{3}{14}$
C.$\frac{7}{6}$
D.$\frac{14}{3}$
答案:
解析:
首先,我们知道原始的比值是$\frac{3}{7}$,这表示比的前项是3的倍数,后项是7的相同的倍数。为了简化计算,我们可以假设这个倍数为1,即前项为3,后项为7。
题目中说后项乘以了$\frac{1}{2}$,那么新的后项就变成了$7 × \frac{1}{2} = \frac{7}{2}$。
前项没有变化,仍然是3。
所以,新的比值就是前项除以新的后项,即$\frac{3}{\frac{7}{2}}$。
进行计算,我们得到新的比值为$\frac{6}{7}$。
答案:
A
首先,我们知道原始的比值是$\frac{3}{7}$,这表示比的前项是3的倍数,后项是7的相同的倍数。为了简化计算,我们可以假设这个倍数为1,即前项为3,后项为7。
题目中说后项乘以了$\frac{1}{2}$,那么新的后项就变成了$7 × \frac{1}{2} = \frac{7}{2}$。
前项没有变化,仍然是3。
所以,新的比值就是前项除以新的后项,即$\frac{3}{\frac{7}{2}}$。
进行计算,我们得到新的比值为$\frac{6}{7}$。
答案:
A
2. 王芳家在庄丽家的南偏东$50^{\circ}$方向上,也可以说庄丽家在王芳家的(
A.北偏西$40^{\circ}$
B.北偏西$50^{\circ}$
C.东偏南$40^{\circ}$
D.东偏南$50^{\circ}$
B
)方向上。A.北偏西$40^{\circ}$
B.北偏西$50^{\circ}$
C.东偏南$40^{\circ}$
D.东偏南$50^{\circ}$
答案:
解析:本题考查的是位置与方向的知识点。当描述一个地点A在地点B的某个方向上时,那么地点B自然就在地点A的相对方向上。南偏东$50^{\circ}$的相对方向是北偏西$50^{\circ}$。
答案:B.北偏西$50^{\circ}$。
答案:B.北偏西$50^{\circ}$。
3. 六(2)班有男生20人,男生和女生的人数比是5:4,全班有(
A.16
B.25
C.36
D.40
C
)人。A.16
B.25
C.36
D.40
答案:
解析:
本题考查的是比例的应用。
已知男生和女生的人数比是5:4,男生有20人。
可以把男生人数看成5份,那么每份就是$20 ÷ 5 = 4$(人)。
女生的人数就是4份,也就是$4 × 4 = 16$(人)。
全班人数就是男生和女生的总和,即$20 + 16 = 36$(人)。
答案:C。
本题考查的是比例的应用。
已知男生和女生的人数比是5:4,男生有20人。
可以把男生人数看成5份,那么每份就是$20 ÷ 5 = 4$(人)。
女生的人数就是4份,也就是$4 × 4 = 16$(人)。
全班人数就是男生和女生的总和,即$20 + 16 = 36$(人)。
答案:C。
4. 一项工程,甲单独做要8天完成,乙单独做要10天完成,两人合做几天后还剩下这项工程的$\frac{1}{4}$?下面列式正确的是(
A.$1÷(\frac{1}{8}+\frac{1}{10})$
B.$\frac{1}{4}÷(\frac{1}{8}+\frac{1}{10})$
C.$(1-\frac{1}{4})÷(\frac{1}{8}+\frac{1}{10})$
D.$(1-\frac{1}{8})÷(\frac{1}{4}+\frac{1}{10})$
C
)。A.$1÷(\frac{1}{8}+\frac{1}{10})$
B.$\frac{1}{4}÷(\frac{1}{8}+\frac{1}{10})$
C.$(1-\frac{1}{4})÷(\frac{1}{8}+\frac{1}{10})$
D.$(1-\frac{1}{8})÷(\frac{1}{4}+\frac{1}{10})$
答案:
把这项工程的工作量看作单位“1”。甲单独做要8天完成,甲的工作效率是$\frac{1}{8}$;乙单独做要10天完成,乙的工作效率是$\frac{1}{10}$。两人合作的工作效率是$\frac{1}{8}+\frac{1}{10}$。
题目要求两人合做几天后还剩下这项工程的$\frac{1}{4}$,则两人需要完成的工作量是$1 - \frac{1}{4}$。
根据工作时间 = 工作量÷工作效率,可得两人合作的时间为$(1 - \frac{1}{4})÷(\frac{1}{8}+\frac{1}{10})$。
所以列式正确的是选项C。
C
题目要求两人合做几天后还剩下这项工程的$\frac{1}{4}$,则两人需要完成的工作量是$1 - \frac{1}{4}$。
根据工作时间 = 工作量÷工作效率,可得两人合作的时间为$(1 - \frac{1}{4})÷(\frac{1}{8}+\frac{1}{10})$。
所以列式正确的是选项C。
C
5. 如图,甲、乙两个完全相同的长方体玻璃缸,缸中水的体积相等,现将两个石子分别放入两个玻璃缸中,甲缸中的水面上升10厘米,乙缸中的水面上升7厘米。甲、乙两个玻璃缸中石子的体积比是(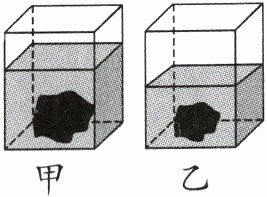
A.7:10
B.10:7
C.1:1
D.17:10
B
)。
A.7:10
B.10:7
C.1:1
D.17:10
答案:
解析:本题考查了长方体的体积计算以及比例的应用。
因为两个玻璃缸完全相同且原来水的体积相等,
放入石子后,水面上升的体积就是石子的体积。
设玻璃缸的底面积为$S$。
甲缸中石子的体积$V_甲$等于水面上升的体积,
即$V_甲 = 10S$。
乙缸中石子的体积$V_乙$同样等于水面上升的体积,
即$V_乙 = 7S$。
那么甲、乙两个玻璃缸中石子的体积比为:
$\frac{V_甲}{V_乙} = \frac{10S}{7S} = \frac{10}{7}$,
即$10:7$。
答案:B。
因为两个玻璃缸完全相同且原来水的体积相等,
放入石子后,水面上升的体积就是石子的体积。
设玻璃缸的底面积为$S$。
甲缸中石子的体积$V_甲$等于水面上升的体积,
即$V_甲 = 10S$。
乙缸中石子的体积$V_乙$同样等于水面上升的体积,
即$V_乙 = 7S$。
那么甲、乙两个玻璃缸中石子的体积比为:
$\frac{V_甲}{V_乙} = \frac{10S}{7S} = \frac{10}{7}$,
即$10:7$。
答案:B。
1. 直接写出得数。(8分)
$1÷\frac{1}{3}=$
$\frac{1}{6}×12=$
$1÷\frac{1}{3}=$
3
$1-\frac{1}{2}-\frac{1}{3}=$$\frac{1}{6}$
$\frac{5}{8}×\frac{2}{3}=$$\frac{5}{12}$
$\frac{5}{6}×(18+\frac{6}{25})=$15$\frac{1}{5}$
$\frac{1}{6}×12=$
2
$\frac{2}{9}÷\frac{3}{5}=$$\frac{10}{27}$
$\frac{1}{2}+\frac{7}{12}=$$\frac{13}{12}$
$(3\frac{1}{3}+\frac{7}{9})×0=$0
答案:
3;$\frac{1}{6}$;$\frac{5}{12}$;15$\frac{1}{5}$;2;$\frac{10}{27}$;$\frac{13}{12}$;0
查看更多完整答案,请扫码查看


