《2025年名师面对面先学后练六年级数学上册人教版评议教辅》

2. $\frac{4}{9}的\frac{3}{5}$最接近(B)。
A.$\frac{1}{5}$　　　
B.$\frac{1}{4}$　　　
C.$\frac{1}{3}$　　　
D.$\frac{1}{2}$

答案： 解析：本题可先根据分数乘法的意义求出$\frac{4}{9}$的$\frac{3}{5}$是多少，再分别计算该结果与各选项的差值，差值最小的即为最接近的选项。
步骤一：计算$\frac{4}{9}$的$\frac{3}{5}$的值
根据分数乘法的运算法则：分数乘分数，用分子相乘的积做分子，分母相乘的积做分母，可得：
$\frac{4}{9}×\frac{3}{5}=\frac{4×3}{9×5}=\frac{12}{45}=\frac{4}{15}$
步骤二：分别计算$\frac{4}{15}$与各选项的差值
选项A：计算$\frac{4}{15}$与$\frac{1}{5}$的差值
先将$\frac{1}{5}$化为分母是$15$的分数，即$\frac{1}{5}=\frac{1×3}{5×3}=\frac{3}{15}$，则$\frac{4}{15}-\frac{3}{15}=\frac{1}{15}$。
选项B：计算$\frac{4}{15}$与$\frac{1}{4}$的差值
先将$\frac{4}{15}$与$\frac{1}{4}$通分，$15$和$4$的最小公倍数是$60$，则$\frac{4}{15}=\frac{4×4}{15×4}=\frac{16}{60}$，$\frac{1}{4}=\frac{1×15}{4×15}=\frac{15}{60}$，所以$\frac{4}{15}-\frac{1}{4}=\frac{16}{60}-\frac{15}{60}=\frac{1}{60}$。
选项C：计算$\frac{4}{15}$与$\frac{1}{3}$的差值
将$\frac{1}{3}$化为分母是$15$的分数，即$\frac{1}{3}=\frac{1×5}{3×5}=\frac{5}{15}$，则$\frac{5}{15}-\frac{4}{15}=\frac{1}{15}$。
选项D：计算$\frac{4}{15}$与$\frac{1}{2}$的差值
$15$和$2$的最小公倍数是$30$，则$\frac{4}{15}=\frac{4×2}{15×2}=\frac{8}{30}$，$\frac{1}{2}=\frac{1×15}{2×15}=\frac{15}{30}$，所以$\frac{1}{2}-\frac{4}{15}=\frac{15}{30}-\frac{8}{30}=\frac{7}{30}$。
步骤三：比较差值大小
将上述差值按照从小到大的顺序排列为：$\frac{1}{60}＜\frac{1}{15}＜\frac{7}{30}$，差值最小的是$\frac{1}{60}$，对应的选项是B。
答案：B

3. 丁丁在计算$(\frac{3}{4}+◯)×\frac{2}{5}$时,算成了$\frac{3}{4}+◯×\frac{2}{5}$,他的计算结果与正确的计算结果相比较,(C)。
A.大0.3　　　
B.小0.3　　　
C.大0.45　　　
D.一样

答案： 设◯为$x$。
正确结果：$(\frac{3}{4} + x)×\frac{2}{5} = \frac{3}{4}×\frac{2}{5} + x×\frac{2}{5} = \frac{3}{10} + \frac{2}{5}x$
错误结果：$\frac{3}{4} + x×\frac{2}{5} = \frac{3}{4} + \frac{2}{5}x$
两者差值：$(\frac{3}{4} + \frac{2}{5}x) - (\frac{3}{10} + \frac{2}{5}x) = \frac{3}{4} - \frac{3}{10} = \frac{15}{20} - \frac{6}{20} = \frac{9}{20} = 0.45$
错误结果比正确结果大$0.45$。
C

4. 把六(1)班的学生调出$\frac{1}{5}$到六(2)班后,六(1)班剩下的学生人数刚好与六(2)班现在的学生人数相等,原来六(2)班的学生人数是六(1)班的(B)。
A.$\frac{4}{5}$　　　
B.$\frac{3}{5}$　　　
C.$\frac{2}{5}$　　　
D.$\frac{1}{5}$

答案： 设六
(1)班原来有学生人数为单位“1”。
调出$\frac{1}{5}$后，六
(1)班剩下人数：$1 - \frac{1}{5} = \frac{4}{5}$。
此时六
(2)班人数等于六
(1)班剩下人数，即六
(2)班现在人数为$\frac{4}{5}$。
六
(2)班原来人数：$\frac{4}{5} - \frac{1}{5} = \frac{3}{5}$。
原来六
(2)班人数是六
(1)班的$\frac{3}{5}$。
答案：B

5. 园林合作社有梨树560棵,______,苹果树有多少棵？列式为$560×(1-\frac{1}{8})$的正确条件是(D)。
A.梨树比苹果树多$\frac{1}{8}$　　　
B.苹果树比梨树多$\frac{1}{8}$
C.梨树比苹果树少$\frac{1}{8}$　　　
D.苹果树比梨树少$\frac{1}{8}$

答案： 解析：
本题考查的是对分数应用题的理解。
题目给出了一个关于梨树和苹果树数量的关系式：$560×(1-\frac{1}{8})$，这个式子表示的是梨树数量乘以一个分数（$1-\frac{1}{8}$）得到的结果。
需要找到一个条件，使得这个关系式能够正确地表示苹果树的数量。
A选项（梨树比苹果树多$\frac{1}{8}$）：
如果梨树比苹果树多$\frac{1}{8}$，那么苹果树的数量应该是梨树数量除以（$1+\frac{1}{8}$），与题目给出的关系式不符。
B选项（苹果树比梨树多$\frac{1}{8}$）：
如果苹果树比梨树多$\frac{1}{8}$，那么苹果树的数量应该是梨树数量乘以（$1+\frac{1}{8}$），同样与题目给出的关系式不符。
C选项（梨树比苹果树少$\frac{1}{8}$）：
如果梨树比苹果树少$\frac{1}{8}$，那么梨树的数量应该是苹果树数量乘以（$1-\frac{1}{8}$），但题目给出的是梨树数量乘以（$1-\frac{1}{8}$），所以这个选项也不对。
D选项（苹果树比梨树少$\frac{1}{8}$）：
如果苹果树比梨树少$\frac{1}{8}$，那么苹果树的数量就应该是梨树数量乘以（$1-\frac{1}{8}$），与题目给出的关系式一致。
所以，正确答案是D。
答案：D。

1. 看图列式计算。(6分)
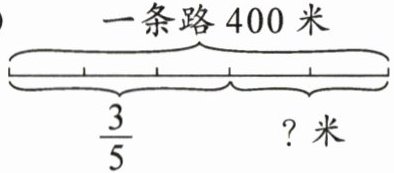
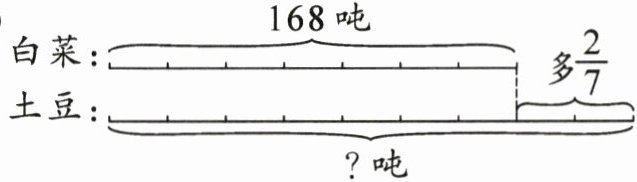
(1)
(2)

答案： 解析：
(1) 本题考查分数的应用。
已知一条路总长400米，其中$\frac{3}{5}$的部分已经给出，需要求剩余部分。
剩余部分为$1-\frac{3}{5}=\frac{2}{5}$。
剩余长度为$400×\frac{2}{5}=160$米。
(2) 本题考查分数的应用。
已知白菜有168吨，土豆比白菜多$\frac{2}{7}$。
土豆比白菜多的量为$168×\frac{2}{7}=48$吨。
土豆的总量为$168+48=216$吨。
答案：
(1) $400×(1-\frac{3}{5})=160$（米）
(2) $168×(1+\frac{2}{7})=216$（吨）

2. 根据算式,先涂一涂,再算一算。(4分)

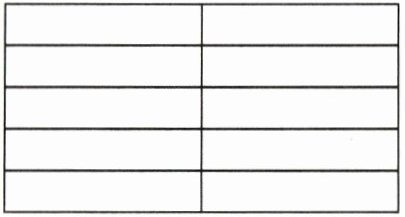
$\frac{4}{5}×\frac{1}{2}=$($\frac{2}{5}$)

答案： 解析：本题考查分数乘法的意义，即求一个分数的几分之几是多少。对于$\frac{4}{5}×\frac{1}{2}$，需要先把一个图形平均分成5份，取其中的4份涂上一种颜色（比如红色），再把这4份看作一个整体，平均分成2份，取其中的1份涂上另一种颜色（比如蓝色），最后数出蓝色部分占整个图形的几分之几，从而得出结果。
答案：图略，$\frac{4}{5}×\frac{1}{2}=\frac{2}{5}$。