1. 圆有
无数
条对称轴,扇形有1
条对称轴。
答案:
解析:本题考查圆和扇形的对称轴数量。圆是一个中心对称图形,任意经过圆心的直线都可以将圆分成两个完全对称的部分,因此圆有无数条对称轴。而扇形只有一条对称轴,即扇形的圆心角平分线所在的直线。
答案:无数,1。
答案:无数,1。
2. 一个圆向右滚动一周后经过的路程如图所示,要画一个同样的圆,圆规两脚间的距离应取(
1
)cm,所画的圆的面积是(3.14
)cm²。
答案:
解析:圆滚动一周的距离就是圆的周长,根据圆的周长公式$C = 2\pi r$($C$表示周长,$r$表示半径),已知圆的周长$C = 6.28$厘米,$\pi$通常取$3.14$,则可求出半径$r$,圆规两脚间的距离就是所画圆的半径,再根据圆的面积公式$S=\pi r^{2}$($S$表示面积)求出圆的面积。
1. 求圆的半径$r$:
已知圆的周长$C = 6.28$厘米,由$C = 2\pi r$可得$r=\frac{C}{2\pi}$,将$C = 6.28$厘米,$\pi = 3.14$代入可得:
$r=\frac{6.28}{2×3.14}= 1$(厘米)
即圆规两脚间的距离应取$1$厘米。
2. 求圆的面积$S$:
由圆的面积公式$S=\pi r^{2}$,将$r = 1$厘米,$\pi = 3.14$代入可得:
$S=3.14×1^{2}=3.14$(平方厘米)
答案:1;3.14。
1. 求圆的半径$r$:
已知圆的周长$C = 6.28$厘米,由$C = 2\pi r$可得$r=\frac{C}{2\pi}$,将$C = 6.28$厘米,$\pi = 3.14$代入可得:
$r=\frac{6.28}{2×3.14}= 1$(厘米)
即圆规两脚间的距离应取$1$厘米。
2. 求圆的面积$S$:
由圆的面积公式$S=\pi r^{2}$,将$r = 1$厘米,$\pi = 3.14$代入可得:
$S=3.14×1^{2}=3.14$(平方厘米)
答案:1;3.14。
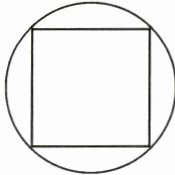
3. 如图所示,正方形的四个顶点均在圆上,已知正方形的对角线长8 cm,圆的周长是(
25.12
)cm,面积是(50.24
)$cm^2$。
答案:
解析:本题考查圆的周长和面积计算,需要先根据正方形对角线长度求出圆的直径,再根据圆的周长和面积公式进行计算。
正方形的四个顶点均在圆上,正方形的对角线就是圆的直径,已知正方形对角线长$8cm$,所以圆的直径$d = 8cm$。
根据圆的周长公式$C=\pi d$(其中$C$表示圆的周长,$\pi$通常取$3.14$,$d$表示圆的直径),可得圆的周长为:$3.14×8 = 25.12(cm)$。
根据圆的半径与直径的关系$r=\frac{d}{2}$(其中$r$表示圆的半径,$d$表示圆的直径),可得圆的半径为:$8÷2 = 4(cm)$。
再根据圆的面积公式$S = \pi r^2$(其中$S$表示圆的面积,$\pi$通常取$3.14$,$r$表示圆的半径),可得圆的面积为:$3.14×4^2 = 3.14×16 = 50.24(cm^2)$。
答案:$25.12$;$50.24$。
正方形的四个顶点均在圆上,正方形的对角线就是圆的直径,已知正方形对角线长$8cm$,所以圆的直径$d = 8cm$。
根据圆的周长公式$C=\pi d$(其中$C$表示圆的周长,$\pi$通常取$3.14$,$d$表示圆的直径),可得圆的周长为:$3.14×8 = 25.12(cm)$。
根据圆的半径与直径的关系$r=\frac{d}{2}$(其中$r$表示圆的半径,$d$表示圆的直径),可得圆的半径为:$8÷2 = 4(cm)$。
再根据圆的面积公式$S = \pi r^2$(其中$S$表示圆的面积,$\pi$通常取$3.14$,$r$表示圆的半径),可得圆的面积为:$3.14×4^2 = 3.14×16 = 50.24(cm^2)$。
答案:$25.12$;$50.24$。
4. 小圆的直径等于大圆的半径,大圆与小圆周长的比是(
2:1
),面积的比是(4:1
)。
答案:
解析:
本题考查的是圆的周长和面积公式的应用。
设小圆的半径为$r$,则小圆的直径为$2r$,大圆的半径为$2r$。
根据圆的周长=$2\pi ×$ 半径,可得:
小圆的周长为:$2\pi r$。
大圆的周长为:$2\pi × 2r=4\pi r$。
大圆周长:小圆周长=$4\pi r:2\pi r=2:1$。
根据圆的面积=$\pi ×$ 半径的平方,可得:
小圆的面积为:$\pi r^{2}$。
大圆的面积为:$\pi × (2r)^{2}=4\pi r^{2}$。
大圆面积:小圆面积=$4\pi r^{2}:\pi r^{2}=4:1$。
答案:
2:1;4:1。
本题考查的是圆的周长和面积公式的应用。
设小圆的半径为$r$,则小圆的直径为$2r$,大圆的半径为$2r$。
根据圆的周长=$2\pi ×$ 半径,可得:
小圆的周长为:$2\pi r$。
大圆的周长为:$2\pi × 2r=4\pi r$。
大圆周长:小圆周长=$4\pi r:2\pi r=2:1$。
根据圆的面积=$\pi ×$ 半径的平方,可得:
小圆的面积为:$\pi r^{2}$。
大圆的面积为:$\pi × (2r)^{2}=4\pi r^{2}$。
大圆面积:小圆面积=$4\pi r^{2}:\pi r^{2}=4:1$。
答案:
2:1;4:1。
5. 在一个长3分米、宽2分米的长方形里剪一个最大的圆,圆的面积是(
3.14
)平方分米,剩下部分的面积是(2.86
)平方分米。
答案:
解析:
在一个长3分米、宽2分米的长方形里剪一个最大的圆,这个圆的直径最大就是长方形的宽,即2分米。因此,圆的半径为1分米。
首先,计算圆的面积。圆的面积公式是$S = \pi r^{2}$,其中r是圆的半径。将r=1代入公式,得到圆的面积为$3.14 × 1^{2} = 3.14(平方分米)$。
然后,计算长方形的面积。长方形面积公式是$S = 长 × 宽$,代入长=3分米,宽=2分米,得到长方形面积为$3 × 2 = 6(平方分米)$。
最后,计算剩下部分的面积。剩下部分的面积就是长方形的面积减去圆的面积,即$6 - 3.14 = 2.86(平方分米)$。
答案:
在一个长3分米、宽2分米的长方形里剪一个最大的圆,圆的面积是(3.14)平方分米,剩下部分的面积是(2.86)平方分米。
在一个长3分米、宽2分米的长方形里剪一个最大的圆,这个圆的直径最大就是长方形的宽,即2分米。因此,圆的半径为1分米。
首先,计算圆的面积。圆的面积公式是$S = \pi r^{2}$,其中r是圆的半径。将r=1代入公式,得到圆的面积为$3.14 × 1^{2} = 3.14(平方分米)$。
然后,计算长方形的面积。长方形面积公式是$S = 长 × 宽$,代入长=3分米,宽=2分米,得到长方形面积为$3 × 2 = 6(平方分米)$。
最后,计算剩下部分的面积。剩下部分的面积就是长方形的面积减去圆的面积,即$6 - 3.14 = 2.86(平方分米)$。
答案:
在一个长3分米、宽2分米的长方形里剪一个最大的圆,圆的面积是(3.14)平方分米,剩下部分的面积是(2.86)平方分米。
6. 如图,小圆的直径是2厘米。
(1)两个小圆的面积之和是大圆面积的$\frac{
(2)两个小圆的周长之和

(1)两个小圆的面积之和是大圆面积的$\frac{
1
}{2
}$。(2)两个小圆的周长之和
等于
大圆的周长。(填“大于”“小于”或“等于”)
答案:
解析:本题可根据圆的面积公式和周长公式分别计算出两个小圆的面积之和、周长之和以及大圆的面积和周长,再进行比较。
(1)求两个小圆的面积之和是大圆面积的几分之几:
已知小圆的直径是$2$厘米,根据圆的直径与半径的关系$r = d÷2$(其中$r$为半径,$d$为直径),可得小圆半径$r_1 = 2÷2 = 1$厘米。
根据圆的面积公式$S = \pi r^2$(其中$S$为面积,$r$为半径),可得一个小圆的面积为:$\pi×1^2=\pi$(平方厘米),那么两个小圆的面积之和为:$2×\pi = 2\pi$(平方厘米)。
由图可知大圆的直径等于两个小圆的直径之和,即大圆直径$d_2 = 2 + 2 = 4$厘米,则大圆半径$r_2 = 4÷2 = 2$厘米。
所以大圆的面积为:$\pi×2^2 = 4\pi$(平方厘米)。
两个小圆的面积之和与大圆面积的比值为:$2\pi÷4\pi=\frac{2\pi}{4\pi}=\frac{1}{2}$。
(2)比较两个小圆的周长之和与大圆的周长:
根据圆的周长公式$C = \pi d$(其中$C$为周长,$d$为直径),一个小圆的直径$d_1 = 2$厘米,则一个小圆的周长为:$\pi×2 = 2\pi$(厘米),那么两个小圆的周长之和为:$2×2\pi = 4\pi$(厘米)。
大圆直径$d_2 = 4$厘米,则大圆的周长为:$\pi×4 = 4\pi$(厘米)。
所以两个小圆的周长之和等于大圆的周长。
答案:
(1)$\frac{1}{2}$;
(2)等于。
(1)求两个小圆的面积之和是大圆面积的几分之几:
已知小圆的直径是$2$厘米,根据圆的直径与半径的关系$r = d÷2$(其中$r$为半径,$d$为直径),可得小圆半径$r_1 = 2÷2 = 1$厘米。
根据圆的面积公式$S = \pi r^2$(其中$S$为面积,$r$为半径),可得一个小圆的面积为:$\pi×1^2=\pi$(平方厘米),那么两个小圆的面积之和为:$2×\pi = 2\pi$(平方厘米)。
由图可知大圆的直径等于两个小圆的直径之和,即大圆直径$d_2 = 2 + 2 = 4$厘米,则大圆半径$r_2 = 4÷2 = 2$厘米。
所以大圆的面积为:$\pi×2^2 = 4\pi$(平方厘米)。
两个小圆的面积之和与大圆面积的比值为:$2\pi÷4\pi=\frac{2\pi}{4\pi}=\frac{1}{2}$。
(2)比较两个小圆的周长之和与大圆的周长:
根据圆的周长公式$C = \pi d$(其中$C$为周长,$d$为直径),一个小圆的直径$d_1 = 2$厘米,则一个小圆的周长为:$\pi×2 = 2\pi$(厘米),那么两个小圆的周长之和为:$2×2\pi = 4\pi$(厘米)。
大圆直径$d_2 = 4$厘米,则大圆的周长为:$\pi×4 = 4\pi$(厘米)。
所以两个小圆的周长之和等于大圆的周长。
答案:
(1)$\frac{1}{2}$;
(2)等于。
7. 一个圆形花坛的直径是40 m,扩建后,半径增加了10 m,这个花坛扩建后的面积增加了(
1570
)m²。
答案:
原半径:40÷2=20(m)
扩建后半径:20+10=30(m)
原面积:3.14×20²=1256(m²)
扩建后面积:3.14×30²=2826(m²)
增加的面积:2826-1256=1570(m²)
1570
扩建后半径:20+10=30(m)
原面积:3.14×20²=1256(m²)
扩建后面积:3.14×30²=2826(m²)
增加的面积:2826-1256=1570(m²)
1570
8. 有一个半圆形的水池,量得它的周长是10.28米,这个水池的半径是(
2
)米,面积是(6.28
)平方米。
答案:
解析:本题主要考查半圆的周长和面积公式。
首先,我们需要理解半圆的周长是如何计算的。
半圆的周长由半圆弧和直径组成。
设半圆的半径为$r$,则半圆弧的长度为$\pi r$($\pi$取3.14),直径的长度为$2r$。
因此,半圆的周长公式为:$C = \pi r + 2r$。
根据题目,这个周长是10.28米。
我们可以建立方程:
$\pi r + 2r = 10.28$,
将$\pi$取3.14代入方程,得到:
$3.14r + 2r = 10.28$,
$5.14r = 10.28$,
$r = \frac{10.28}{5.14}$,
$r = 2$。
接下来,我们计算半圆的面积。
半圆的面积公式是:$S = \frac{1}{2} \pi r^{2}$。
将$r = 2$代入公式,得到:
$S = \frac{1}{2} × 3.14 × 2^{2}$,
$S = \frac{1}{2} × 3.14 × 4$,
$S = 6.28$(平方米)。
答案:2;6.28。
首先,我们需要理解半圆的周长是如何计算的。
半圆的周长由半圆弧和直径组成。
设半圆的半径为$r$,则半圆弧的长度为$\pi r$($\pi$取3.14),直径的长度为$2r$。
因此,半圆的周长公式为:$C = \pi r + 2r$。
根据题目,这个周长是10.28米。
我们可以建立方程:
$\pi r + 2r = 10.28$,
将$\pi$取3.14代入方程,得到:
$3.14r + 2r = 10.28$,
$5.14r = 10.28$,
$r = \frac{10.28}{5.14}$,
$r = 2$。
接下来,我们计算半圆的面积。
半圆的面积公式是:$S = \frac{1}{2} \pi r^{2}$。
将$r = 2$代入公式,得到:
$S = \frac{1}{2} × 3.14 × 2^{2}$,
$S = \frac{1}{2} × 3.14 × 4$,
$S = 6.28$(平方米)。
答案:2;6.28。
9. 将一个直径是4 dm的圆等分成若干份并沿半径剪开,再拼成一个近似的长方形,这个长方形的周长是(
16.56
)dm,面积是(12.56
)$dm^2。$
答案:
圆的半径:4÷2=2(dm)
长方形的长:3.14×4÷2=6.28(dm)
长方形的宽:2 dm
长方形的周长:(6.28+2)×2=16.56(dm)
长方形的面积:6.28×2=12.56(dm²)
16.56;12.56
长方形的长:3.14×4÷2=6.28(dm)
长方形的宽:2 dm
长方形的周长:(6.28+2)×2=16.56(dm)
长方形的面积:6.28×2=12.56(dm²)
16.56;12.56
10. 如图,大半圆的直径是10 cm,小半圆的直径是4 cm,阴影部分的周长是(
28.26
)cm,面积是(26.69
)$cm^2$。
答案:
周长:3.14×10÷2 + 3.14×4 = 15.7 + 12.56 = 28.26(cm)
面积:3.14×(10÷2)²÷2 - 3.14×(4÷2)² = 39.25 - 12.56 = 26.69(cm²)
答案:28.26;26.69
面积:3.14×(10÷2)²÷2 - 3.14×(4÷2)² = 39.25 - 12.56 = 26.69(cm²)
答案:28.26;26.69
二、判断题。(对的画“√”,错的画“×”)(5分)
1. 通过圆心且两端都在圆上的线段叫作直径。(
2. 当圆的半径为2分米时,这个圆的周长和面积相等。(
3. 所有圆的周长和它的直径的比值都相等。(
4. 两个半圆一定可以拼成一个整圆。(
5. 圆的面积比扇形的面积大。(
1. 通过圆心且两端都在圆上的线段叫作直径。(
√
)2. 当圆的半径为2分米时,这个圆的周长和面积相等。(
×
)3. 所有圆的周长和它的直径的比值都相等。(
√
)4. 两个半圆一定可以拼成一个整圆。(
×
)5. 圆的面积比扇形的面积大。(
×
)
答案:
解析:
1. 本题考查圆的直径的定义,根据定义,通过圆心且两端都在圆上的线段叫作直径,所以此题正确。
2. 本题考查圆的周长和面积的意义,周长是长度,单位是分米,面积是大小,单位是平方分米,两者不能比较,所以此题错误。
3. 本题考查圆的周长和直径的关系,所有圆的周长和它的直径的比值都相等,都等于圆周率$\pi$,所以此题正确。
4. 本题考查圆的特征,只有两个完全相同的半圆才能拼成一个整圆,所以此题错误。
5. 本题考查圆和扇形的面积,在半径不确定的情况下,无法比较圆的面积和扇形的面积的大小,所以此题错误。
答案:√;×;√;×;×。
1. 本题考查圆的直径的定义,根据定义,通过圆心且两端都在圆上的线段叫作直径,所以此题正确。
2. 本题考查圆的周长和面积的意义,周长是长度,单位是分米,面积是大小,单位是平方分米,两者不能比较,所以此题错误。
3. 本题考查圆的周长和直径的关系,所有圆的周长和它的直径的比值都相等,都等于圆周率$\pi$,所以此题正确。
4. 本题考查圆的特征,只有两个完全相同的半圆才能拼成一个整圆,所以此题错误。
5. 本题考查圆和扇形的面积,在半径不确定的情况下,无法比较圆的面积和扇形的面积的大小,所以此题错误。
答案:√;×;√;×;×。
查看更多完整答案,请扫码查看


