搜索
一、【例题仿练】看图填一填。
1.如右图,圆上A、B两点之间的部分叫作( ),读作"( )"。
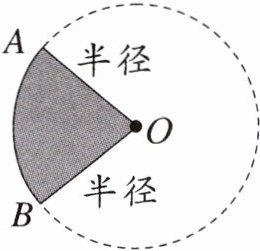
2.由半径OA、OB和弧AB围成的阴影部分叫作( ),∠AOB叫作( )。
【总结】圆上两点之间的部分叫作( ),一条弧和经过这条弧的两条半径所围成的图形叫作( )。顶点在( )的角叫作圆心角,同一圆中,扇形的大小与这个扇形的( )有关,圆心角越大,扇形( )。
1.如右图,圆上A、B两点之间的部分叫作( ),读作"( )"。
2.由半径OA、OB和弧AB围成的阴影部分叫作( ),∠AOB叫作( )。
【总结】圆上两点之间的部分叫作( ),一条弧和经过这条弧的两条半径所围成的图形叫作( )。顶点在( )的角叫作圆心角,同一圆中,扇形的大小与这个扇形的( )有关,圆心角越大,扇形( )。
答案：
1.弧 弧AB 2.扇形 圆心角 总结:弧 扇形 圆心 圆心角的大小 越大
二、判断题。(对的画"√",错的画"×")
1.扇形有无数条对称轴。( )
2.两条线段和一条弧围成的图形叫作扇形。( )
3.在一个圆中剪去一个扇形后,剩下的部分一定是扇形。( )
1.扇形有无数条对称轴。( )
2.两条线段和一条弧围成的图形叫作扇形。( )
3.在一个圆中剪去一个扇形后,剩下的部分一定是扇形。( )
答案：
1.× 2.× 3.√
三、下面哪个图形的涂色部分是扇形?在是的( )里画"√",不是的( )里画"×"。
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
答案：
× √ √ ×
四、下面图形中哪些角是圆心角?在( )里画"√"。
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
答案：
( )(√)( )(√)
五、画一个直径是3 cm的圆,再在圆中画一个圆心角是120°的扇形,并求出扇形的面积。
答案：
120÷360=$\frac{1}{3}$ 3.14×(3÷2)²×$\frac{1}{3}$=2.355(cm²)
解析依题意，求圆内的圆心角是120°的扇形的面积，应先求出扇形是所在圆的几分之几，即120÷360=$\frac{1}{3}$，再求这个扇形的面积，就是求所在圆面积的$\frac{1}{3}$是多少，即3.14×(3÷2)²×$\frac{1}{3}$=2.355(cm²)。
120÷360=$\frac{1}{3}$ 3.14×(3÷2)²×$\frac{1}{3}$=2.355(cm²)
解析依题意，求圆内的圆心角是120°的扇形的面积，应先求出扇形是所在圆的几分之几，即120÷360=$\frac{1}{3}$，再求这个扇形的面积，就是求所在圆面积的$\frac{1}{3}$是多少，即3.14×(3÷2)²×$\frac{1}{3}$=2.355(cm²)。 六、求下图中阴影部分的面积。
1.
2.
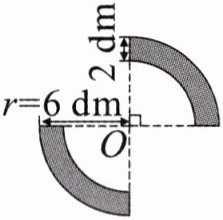
1.
2.
答案：
1.3.14×10²×$\frac{1}{2}$=157(cm²) 2.6−2=4(dm) 3.14×(6²−4²)×$\frac{1}{2}$=31.4(dm²) 解析1.三个圆心连接成一个三角形，三角形内角和为180°，三个圆心角之和为180°，它们可以拼成一个圆心角是180°的扇形，也就是半圆，所以阴影部分的面积是3.14×10²×$\frac{1}{2}$=157(cm²)。 2.阴影部分是2个圆心角是90°的扇环，可以拼成圆环的一半，外半径是6dm，环宽是2dm，则内半径是6−2=4(dm)，所以阴影部分的面积是3.14×(6²−4²)×$\frac{1}{2}$=31.4(dm²)。
七、【拓展题】右下图是一个等腰直角三角形,虚线表示等腰三角形的高,也是扇形的半径,求图中阴影部分的面积。
答案：
10×10÷2×2−3.14×10²×$\frac{1}{4}$=21.5(cm²) 解析观察题图发现，阴影部分的面积等于大等腰直角三角形的面积减去圆心角为90°的扇形的面积。题中等腰直角三角形可以分割成两个小直角三角形，虚线表示大等腰直角三角形的高，因为大等腰直角三角形两底角是45°，所以两个小直角三角形也是等腰直角三角形，小三角形的两条直角边等于扇形的半径，大三角形的面积是10×10 ÷2×2=100(cm²)。圆心角是90°的扇形的面积等于所在圆的面积的$\frac{1}{4}$，即3.14×10²×$\frac{1}{4}$=78.5(cm²)，所以阴影部分的面积是100−78.5 =21.5(cm²)。
查看更多完整答案，请扫码查看
