《2025年名师面对面先学后练六年级数学上册人教版》

1.用一张边长是8 dm的正方形纸片,剪一些半径是1 dm的圆片,一共可以剪( )个。

答案： 16 解析 1.半径是1 dm的圆片,直径是1×2=2(dm),边长8 dm的正方形,每排最多可以剪8÷2=4(个)圆,剪4排,一共可以剪4×4=16(个)。

2.一个时钟的分针长4 cm,从9:00到9:45分针尖端走过的路程是( )cm,扫过的面积是( )$cm^{2}$。

答案： 18.84 37.68 解析 2.由题意可知,分针长4 cm,从9:00到9:45,分针尖端走过的路程是半径为4 cm的圆的周长的$\frac{3}{4}$,扫过的面积是半径为4 cm的圆面积的$\frac{3}{4}$,所以分针尖端走过的路程是$2×3.14×4×\frac{3}{4}=18.84$(cm),扫过的面积是$3.14×4^{2}×\frac{3}{4}=37.68$(cm²)。

3.一个圆环的内圆直径是6 cm,外圆直径是8 cm,它的面积是( )$cm^{2}$。

答案： 21.98 解析 3.圆环内圆直径是6 cm,则内圆半径是6÷2=3(cm),外圆直径是8 m,则外圆半径是8÷2=4(cm),根据圆环的面积公式$S=π(R^{2}-r^{2})$计算,它的面积是$3.14×(4^{2}-3^{2})=21.98$(cm²)。

1.一个圆的半径扩大到原来的4倍,它的面积扩大到原来的( )倍。

A.2
B.4
C.16

答案： C 解析 1.圆的面积是$πr^{2}$,半径扩大到原来的4倍,面积为$π×(4r)^{2}=16πr^{2}$,所以面积扩大到原来的16倍。

2.圆的半径由5 dm增加到7 dm,圆的面积增加了( )$dm^{2}$。

A.$2\pi$
B.24
C.$24\pi$

答案： C 解析 2.半径为5 dm的圆的面积是$π×5^{2}=25π$(dm²),半径增加到7 dm后圆的面积是$π×7^{2}=49π$(dm²),面积增加了$49π-25π=24π$(dm²)。

3.从一张正方形的纸片中剪下一个最大的圆,这个圆的面积是正方形面积的( )。

A.$\frac{1}{2}$
B.$\frac{1}{4}$
C.$\frac{\pi}{4}$

答案： C 解析 3.从一张正方形纸上剪下一个最大的圆,正方形的边长等于圆的直径,圆的面积是$πr^{2}$,正方形的面积是$(2r)×(2r)=4r^{2}$,圆的面积是正方形面积的$\frac{πr^{2}}{4r^{2}}$,化简得$\frac{π}{4}$。

三、求下图中阴影部分的周长和面积。(单位:cm)
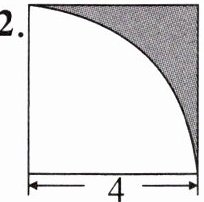
1.
2.

答案： 1.周长:$3.14×(2+2)=12.56$(cm) 面积:$(2+2)^{2}-3.14×2^{2}=3.44$(cm²) 解析 观察题图可知,$\frac{1}{4}$圆的半径是2 cm,正方形的边长是(2+2)cm,阴影部分的周长为4条曲线长度之和,等于半径为2 cm圆的周长,可以直接利用圆的周长公式计算。阴影部分的面积等于正方形面积减去4个$\frac{1}{4}$圆(合成一个整圆)的面积。 2.周长:$3.14×4×2×\frac{1}{4}+4×2=14.28$(cm) 面积:$4×4-3.14×4^{2}÷4=3.44$(cm²) 解析 观察题图可知,正方形边长为4 cm,阴影部分的周长等于半径为4 cm的圆的周长的$\frac{1}{4}$加上正方形的两条边长,所以阴影部分的周长为$3.14×4×2×\frac{1}{4}+4×2=14.28$(cm)。阴影部分的面积等于正方形面积减去$\frac{1}{4}$圆的面积,即$4×4-3.14×4^{2}÷4=3.44$(cm²)。

四、右下图是我国古代房屋墙上安装的木窗。正方形木框的边长是1米,外面的正方形与内部的圆之间的面积是多少?

答案： $1×1-3.14×(1÷2)^{2}=0.215$(平方米) 解析 本题是一道外方内圆的实际问题,正方形与圆之间部分的面积=正方形的面积-圆的面积,已知正方形边长(圆的直径)是1 m,那么正方形的面积是1×1=1(m²),圆的面积是$3.14×(1÷2)^{2}=0.785$(m²),正方形与圆之间部分的面积是1-0.785=0.215(m²)。

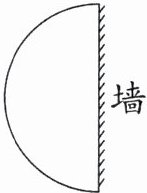
五、王大爷用25.12 m长的篱笆靠墙围成一个半圆形鸡舍,这个鸡舍的面积是多少平方米?

答案： $25.12÷3.14=8$(m) $3.14×8^{2}÷2=100.48$(m²) 解析 靠墙围成一个半圆形鸡舍,篱笆长25.12 m,也就是圆周长的一半是25.12 m,即$πr=25.12$,可以求出这个半圆形鸡舍的半径是25.12÷3.14=8(m)。所以半圆形鸡舍的面积是$3.14×8^{2}÷2=100.48$(m²)。

六、地面上平躺着一个底面半径为0.5 m的圆柱形油桶,如果将这个油桶滚到墙边(如下图所示),需要滚动几周?

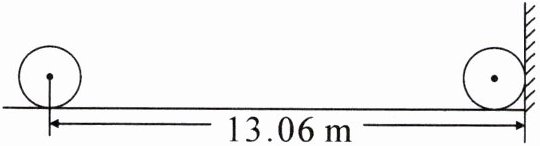
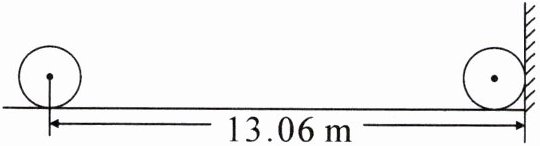
答案： $13.06-0.5=12.56$(m) $12.56÷(2×3.14×0.5)=4$(周) 解析 观察题图可知,油桶滚到墙边,油桶靠着墙,滚动的长度是13.06-0.5=12.56(m),油桶滚动一周的长度是$2×3.14×0.5=3.14$(m),所以需要滚动12.56÷3.14=4(周)。

七、【拓展题】如右下图,正方形的面积是8平方厘米,求图中阴影部分的面积。

答案： $3.14×8×(1-\frac{1}{4})=18.84$(cm²) 解析 观察题图可知,正方形的边长等于圆的半径,假设圆的半径为r cm,由正方形的面积是8平方厘米,得$r^{2}=8$,阴影部分的面积等于圆的面积的$(1-\frac{1}{4})$,所以阴影部分的面积是$3.14×8×(1-\frac{1}{4})=18.84$(cm²)。