一、【例题仿练】看图填一填。
1. 涂色部分是一个( )。
2. 外圆的面积= ( )cm^2,内圆的面积= ( )cm^2,圆环的面积= ( )-( )= ( )cm^2。

【总结】圆环的面积:$S= \pi R^{2}-\pi r^{2}= \pi (R^{2}-r^{2})$
1. 涂色部分是一个( )。
2. 外圆的面积= ( )cm^2,内圆的面积= ( )cm^2,圆环的面积= ( )-( )= ( )cm^2。

【总结】圆环的面积:$S= \pi R^{2}-\pi r^{2}= \pi (R^{2}-r^{2})$
答案:
1.圆环 2.200.96 113.04 200.96 113.04 87.92
1. 小圆的直径和大圆的半径相等,小圆面积是大圆面积的( )。
A.$\frac{1}{2}$
B.$\frac{1}{4}$
C.$\frac{1}{6}$
A.$\frac{1}{2}$
B.$\frac{1}{4}$
C.$\frac{1}{6}$
答案:
B
2. 一个圆环,内圆半径是4cm,外圆半径是5cm,计算这个圆环面积错误的算式是( )。
A.$3.14× (5^{2}-4^{2})$
B.$3.14× (5-4)^{2}$
C.$3.14× 5^{2}-3.14× 4^{2}$
A.$3.14× (5^{2}-4^{2})$
B.$3.14× (5-4)^{2}$
C.$3.14× 5^{2}-3.14× 4^{2}$
答案:
B
三、求下图中阴影部分的面积。(单位:cm)


答案:
1.3.14×(4²-2²)=37.68(cm²) 2.3.14×[(6÷2+2)²-(6÷2)²]=50.24(cm²)
四、学校草地上原来有一个射程是20米的自动旋转洒水器,新学期更换了新的自动旋转洒水器,射程达到25米。喷洒面积增加了多少平方米?


答案:
3.14×(25²-20²)=706.5(平方米)
五、求出右下面图形的周长和面积。(单位:m)
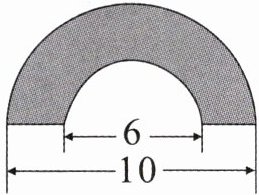

答案:
周长:3.14×(6+10)÷2+(10-6)=29.12(m) 面积:10÷2=5(m) 6÷2=3(m) 3.14×(5²-3²)÷2=25.12(m²)
六、在一个周长为62.8米的圆形花坛周围铺一条2米宽的小路,小路的面积是多少平方米?
答案:
62.8÷3.14÷2=10(米) 10+2=12(米) 3.14×(12²-10²)=138.16(平方米)
七、右下图中,阴影部分的面积是$40cm^2,$圆环的面积是多少平方厘米?
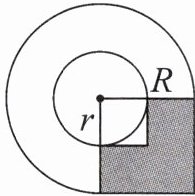

答案:
阴影部分的面积=R²-r²=40(cm²) 圆环的面积=π(R²-r²)=3.14×40=125.6(cm²)
八、【拓展题】如右下图,三个同心圆的半径之比是1:3:5,则阴影部分与空白部分的面积比是多少?
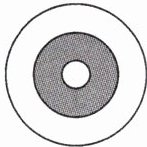

答案:
设小圆半径为r。阴影部分的面积:π×(3r)²-πr²=8πr² 空白部分的面积:π×(5r)²-8πr²=17πr² 8πr²:17πr²=8:17
查看更多完整答案,请扫码查看


