《2025年名师面对面先学后练六年级数学上册人教版》

一、【例题仿练】看图列式计算。(用两种方法计算)

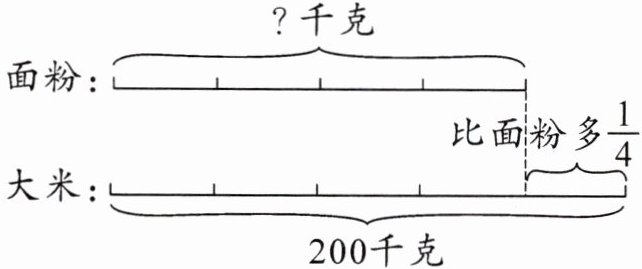
【总结】根据题中的等量关系"单位'1'的量×(1±几分之几)= 已知量"或"单位'1'的量±单位'1'的量×几分之几= 已知量",设单位"1"的量为x,列方程解答。

答案： 方法一:解:设面粉质量为x千克。
(1+$\frac{1}{4}$)x=200
x=160
方法二:解:设面粉质量为x千克。
x+$\frac{1}{4}$x=200
x=160
解析 观察线段图可知,大米有200千克,比面粉多$\frac{1}{4}$。把面粉质量看作单位“1”,大米有200千克,是单位“1”的(1+$\frac{1}{4}$),可以列出等量关系“面粉的质量×(1+$\frac{1}{4}$)=大米的质量”,设食堂有面粉x千克,根据等量关系列方程(1+$\frac{1}{4}$)x=200,解方程得x=160,即为面粉质量。还可以根据“大米比面粉多$\frac{1}{4}$”分析,把面粉的质量看作单位“1”,那么大米的质量=面粉的质量+面粉的质量×$\frac{1}{4}$=200千克。设面粉质量为x千克,根据等量关系可列出方程x+$\frac{1}{4}$x=200,解得x=160,即为面粉质量。

二、中国文学家莫言、药学家屠呦呦都获得了诺贝尔奖。莫言的获奖感言有6300个字,比屠呦呦的获奖感言多$\frac{4}{5}$,屠呦呦的获奖感言有多少个字？(用两种方法解答)

答案： 方法一:解:设屠呦呦的获奖感言有x个字。
x+$\frac{4}{5}$x=6300
x=3500
方法二:6300÷(1+$\frac{4}{5}$)=3500(个)
解析 根据“莫言获奖感言字数比屠呦呦多$\frac{4}{5}$”,可以列出等量关系:屠呦呦获奖感言字数+屠呦呦获奖感言字数×$\frac{4}{5}$=莫言获奖感言字数,再根据等量关系式列方程解答。还可以根据“莫言获奖感言字数是屠呦呦获奖感言字数的(1+$\frac{4}{5}$)”,列除法算式计算,屠呦呦获奖感言字数有6300÷(1+$\frac{4}{5}$)=3500(个)。

三、一辆汽车从甲地开往乙地,行驶了全程的$\frac{3}{8}$,离乙地还有60千米。甲、乙两地相距多少千米？

答案： 解:设甲、乙两地相距x千米。
x-$\frac{3}{8}$x=60
x=96
解析 由题中条件已找到等量关系式:甲、乙两地间的总路程-已行的路程=剩下的路程,设甲、乙两地相距x千米,可列方程x-$\frac{3}{8}$x=60,解得x=96,所以甲、乙两地相距96千米。

四、水结成冰后,体积增加了$\frac{1}{10}$。一块体积是$165\ dm^3$的冰化成水后,体积是多少？

答案： 解:设体积是x dm³。
(1+$\frac{1}{10}$)x=165
x=150
解析 体积增加了$\frac{1}{10}$,则增加后的体积为原来的(1+$\frac{1}{10}$)倍。

五、【拓展题】春节期间,妈妈给小明买了一套衣服,比原价降低了$\frac{1}{5}$。这套衣服降价多少元？

现价：180元

答案： 解:设原价为x元。
x-$\frac{1}{5}$x=180
x=225 225×$\frac{1}{5}$=45(元)
解析 由题中条件可知,这套衣服比原价降了$\frac{1}{5}$,求这套衣服降价多少元,就是求原价的$\frac{1}{5}$是多少,所以先根据等量关系“原价-原价×$\frac{1}{5}$=现价”列方程x-$\frac{1}{5}$x=180并求解,得出原价是225元,再求降价多少元,列式为225×$\frac{1}{5}$。