《2025年口算题卡升级练五年级数学上册人教版》

1 根据平行四边形的相关条件,填一填。
① $a= 50\ \text{cm},h= 5\ \text{dm},S= $$25\ \text{dm}^2$。 ② $S= 400\ \text{dm}^2,a= 0.5\ \text{m},h= $$80\ \text{dm}$。
③ $a= 90\ \text{dm},h= 1\ \text{m},S= $$900\ \text{dm}^2$。 ④ $S= 96\ \text{cm}^2,h= 1.2\ \text{dm},a= $$8\ \text{cm}$。

答案： 解析：本题主要考查平行四边形的面积公式$S = a× h$（其中$S$表示面积，$a$表示底边长，$h$表示这条底边对应的高），在计算时需要注意单位的统一。
①已知$a = 50\ \text{cm}$，因为$1\ \text{dm}=10\ \text{cm}$，所以$50\ \text{cm}=5\ \text{dm}$，$h = 5\ \text{dm}$，根据面积公式可得$S=a× h = 5×5 = 25\ (\text{dm}^2)$。
②已知$S = 400\ \text{dm}^2$，$a = 0.5\ \text{m}$，因为$1\ \text{m}=10\ \text{dm}$，所以$0.5\ \text{m}=5\ \text{dm}$，由$h=\frac{S}{a}$可得$h=\frac{400}{5}=80\ (\text{dm})$。
③已知$a = 90\ \text{dm}$，$h = 1\ \text{m}$，$1\ \text{m}=10\ \text{dm}$，根据面积公式$S=a× h = 90×10 = 900\ (\text{dm}^2)$。
④已知$S = 96\ \text{cm}^2$，$h = 1.2\ \text{dm}$，$1.2\ \text{dm}=12\ \text{cm}$，由$a=\frac{S}{h}$可得$a=\frac{96}{12}=8\ (\text{cm})$。
答案：
①$25\ \text{dm}^2$；
②$80\ \text{dm}$；
③$900\ \text{dm}^2$；
④$8\ \text{cm}$。

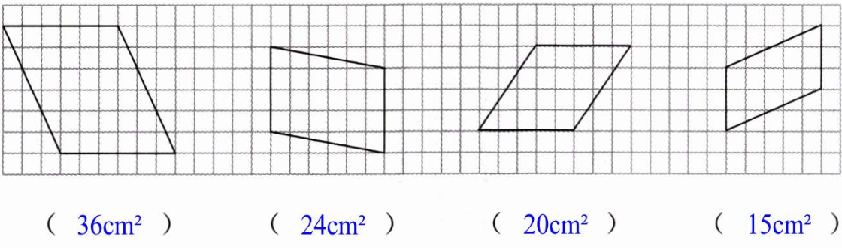
2 把各图形的面积填在( )里。(每个小方格的边长是1 cm。)

( ) ( ) ( ) ( )

答案：

3 计算下面每个平行四边形的面积。

答案： ① 8×3=24(cm²)
② 4×4.8=19.2(dm²)
③ 3.5×4.2=14.7(m²)

4 解决问题。
① 一块平行四边形木板的底是12 dm,高是8 dm。这块木板的面积是多少平方分米?
② 一个平行四边形的高是1.5 m,底是高的1.2倍。这个平行四边形的面积是多少平方米?

答案： 解析：本题考查平行四边形面积的计算。
① 对于第一个问题：
已知平行四边形的底长为 $12 \text{ dm}$，高为 $8\text{ dm}$。
根据平行四边形的面积公式：
$\text{面积} = \text{底} × \text{高}$
代入已知数值进行计算：
$12 × 8 = 96 (\text{平方分米})$
② 对于第二个问题：
已知平行四边形的高为 $1.5 \text{ m}$，底是高的 $1.2$ 倍。
首先计算底长：
$\text{底} = 1.5 × 1.2 = 1.8 (\text{ m})$
再根据平行四边形的面积公式：
$\text{面积} = \text{底} × \text{高}$
代入已知数值进行计算：
$1.8 × 1.5 = 2.7 (\text{平方米})$
答案：① $96 \text{ 平方分米}$；② $2.7\text{ 平方米}$。