《2025年孟建平小学滚动测试六年级数学上册人教版》

1. 在( )里填上合适的数。
$\frac{11}{25}$平方米= ( )平方分米
10 分= ( )时

答案： 44 $\frac{1}{6}$ 名师点评:本题考查单位换算。掌握各类单位间的进率是解本题的关键。

2. 比较大小。
$A÷\frac{98}{99}◯ A(A＞0)$
$3.14×\frac{2021}{2022}◯3.14×\frac{21}{22}$

答案： ＞ ＞

3. 礼品店用$\frac{18}{5}$米的丝带正好包装 6 个盒子,平均每个盒子所用丝带占全部的$\frac{( )}{( )}$,每个盒子用$\frac{( )}{( )}$米丝带。

答案： $\frac{1}{6}$ $\frac{3}{5}$ 解析:每个盒子所用丝带占全部的$1÷6=\frac{1}{6}$,每个盒子用$\frac{1}{6}×\frac{18}{5}=\frac{3}{5}$(米)丝带。

4. 小月读了一本书的$\frac{3}{7}$,还剩 120 页,这本书一共有( )页。(1 分)

答案： 210 解析:这本书一共有$120÷(1-\frac{3}{7})=210$(页)。

5. 红红在解决“已知小明$\frac{2}{3}$小时走了 2 千米,求小明每小时走多少千米?”这个问题时,她是用画线段图的方法来帮助思考(如图),并列式计算:$2÷\frac{2}{3}= 2×\frac{1}{2}×3= 3$(千米)。根据线段图,“$2×\frac{1}{2}$”这一步表示的是小明( )小时走了( )千米。

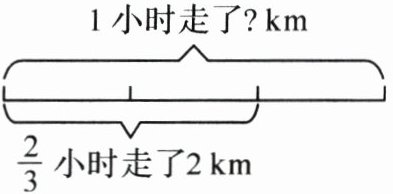
答案： $\frac{1}{3}$ 1

6. 甲数的$\frac{2}{3}$与乙数的和是 60,甲数的$\frac{4}{9}$正好等于乙数,甲、乙两数的和是( )。

答案： 78 解析:因为甲数的$\frac{4}{9}$正好等于乙数,甲数的$\frac{2}{3}$与乙数的和是60,即甲数的$\frac{2}{3}+$甲数的$\frac{4}{9}=60$,所以甲数是$60÷(\frac{4}{9}+\frac{2}{3})=54$,乙数是$54×\frac{4}{9}=24$,则甲、乙两数的和是$54+24=78$。

7. 一个书架分上、中、下三层,上层有 60 本书,中层比上层多$\frac{1}{5}$,中层有( )本书;中层比下层少$\frac{1}{5}$,下层有( )本书。

答案： 72 90 解析:中层有$60×(1+\frac{1}{5})=72$(本)书;下层有$72÷(1-\frac{1}{5})=90$(本)书。

8. 已知$\frac{4}{3}×a= b÷\frac{4}{5}= c÷0.2= d×\frac{5}{6}$,且 a、b、c、d 四个数均不为 0。那么在这四个数中,最大的数是( ),最小的数是( )。

答案： d c 解析:令$\frac{4}{3}×a=b÷\frac{4}{5}=c÷0.2=d×\frac{5}{6}=1$,则$a=\frac{3}{4}$,$b=\frac{4}{5}$,$c=0.2$,$d=\frac{6}{5}$,因为$\frac{6}{5}＞\frac{4}{5}＞\frac{3}{4}＞0.2$,所以四个数中,d最大,c最小。

9. 如图,阴影部分面积占大平行四边形面积的$\frac{1}{12}$,占小平行四边形面积的$\frac{1}{8}$。则小平行四边形的面积是大平行四边形的$\frac{( )}{( )}$。

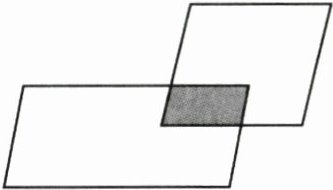
答案： $\frac{2}{3}$ 解析:因为阴影部分是公共的,所以大平行四边形的面积$×\frac{1}{12}=$小平行四边形的面积$×\frac{1}{8}$,则小平行四边形的面积是大平行四边形的$\frac{1}{12}÷\frac{1}{8}=\frac{2}{3}$。

10. 加工一批零件,甲单独做要 7 小时,乙单独做要 9 小时。如果甲、乙两人合作,1 小时能做这批零件的$\frac{( )}{( )}$。如果合作加工完这批零件,需要( )小时。

答案： $\frac{16}{63}$ $\frac{63}{16}$ 解析:甲的工作效率是$\frac{1}{7}$,乙的工作效率是$\frac{1}{9}$。甲、乙合作1小时,工作总量是$(\frac{1}{7}+\frac{1}{9})×1=\frac{16}{63}$,完成这批零件需要$1÷\frac{16}{63}=\frac{63}{16}$(时)。