《2025年孟建平小学滚动测试六年级数学上册人教版》

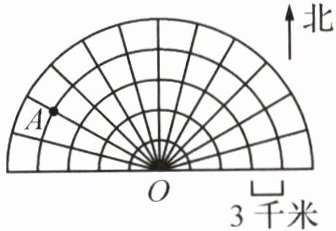
1. 如图,点A在点O的( )偏( )( )度方向上,距离是( )千米。(2分)

答案： 西 北 30(或北 西 60) 12

2. 一根一尺长的木棒,第一天取它的一半,第二天取剩下的一半……这样取下去,五天后剩下的长度是多少尺?(4分)

答案： $1×(1-\frac{1}{2})×(1-\frac{1}{2})×(1-\frac{1}{2})×(1-\frac{1}{2})×(1-\frac{1}{2})=\frac{1}{32}$(尺) 答:五天后剩下的长度是$\frac{1}{32}$尺。

3. 一艘轮船在大海中以每小时16千米的速度向正东方向航行,10时发现北偏东30°方向24千米处有一座灯塔,11时30分这座灯塔在轮船的什么位置?(请描述出准确位置)(4分)

答案：
11时30分-10时=1时30分 1时30分=1.5时 $16×1.5=24$(千米) $90^{\circ}-30^{\circ}=60^{\circ}$ 答:11时30分这座灯塔在轮船的西偏北60°方向24千米处。解析:由题意,从10时到11时30分经过1时30分,即1.5时,轮船向正东方向行驶了$16×1.5=24$(千米)。画出示意,由图可知,$OA=OB=24$千米,且$\angle AOB=90^{\circ}-30^{\circ}=60^{\circ}$,那么三角形AOB是等边三角形,则$AB=24$千米,$\angle ABO=60^{\circ}$,因此11时30分这座灯塔在轮船西偏北60°方向24千米处。