《2025年学霸四年级数学上册人教版》

例1 林真此时在点A的位置,距离b岸边正好是4米,请你帮他设计一条线路,使他游泳时距离b岸边始终是4米。

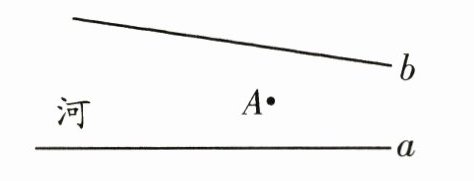
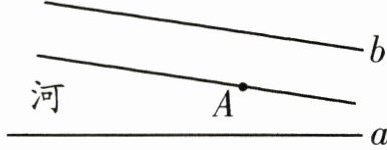
分析:林真的游泳线路距离b岸边的距离始终是4米,说明林真的游泳线路与b岸边恰巧构成一组平行线,并且两条平行线间的距离是4米,可过点A作b岸边的平行线,就是林真的游泳路线。
解
答:

答案： 过点 $A$ 作一条与 $b$ 岸边平行的直线，该直线即为林真的游泳路线。
（在图中，过点 $A$ 作一条与 $b$ 岸边平行的直线即可）。

1. 池塘里有2只小鸭在游泳。
(1)小鸭贝贝想上岸了,它怎样上岸最近？画出它的游泳路线。
(2)小鸭卡卡怎样游,才能使它与西岸的距离一直相等？画出它的游泳路线。

答案：
1.
(1)
(2)如图所示。
　　
提示:由题图可知，贝贝离东岸的距离最短，所以过点作垂直于东岸的垂直线段即可。卡卡的游泳路线与西岸的距离一直相等，说明卡卡的游泳路线与西岸恰巧构成一组平行线，且经过卡卡现在所在的位置。

例2 如图,一辆汽车在一条笔直的公路AB上由点A向点B行驶,点M、N分别是位于公路AB同一侧的两个村庄。

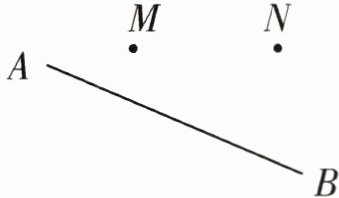
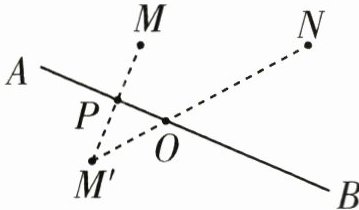
设汽车行驶到公路AB上点O的位置时,到两个村庄的距离之和最小。请在图中画出点O的位置。
分析:两点之间线段最短,已知M、N两个村庄在公路的同一侧。可以假设把村庄M搬到公路的另一侧,过点M向AB画一条垂线,在垂线上找到点M',使点M'到直线AB的距离与点M到直线AB的距离相等,此时M'为点M关于直线AB的对称点。连接M'N,与直线AB相交于一点,此点即为O。除了找点M的对称点,也可以找点N的对称点。确定点O位置的画法不唯一。
解
答:画法不唯一,如:

答案： 1. 过点 $ M $ 作 $ MP \perp AB $，垂足为 $ P $。
2. 延长 $ MP $ 至 $ M' $，使 $ M'P = MP $，即 $ M' $ 为 $ M $ 关于直线 $ AB $ 的对称点。
3. 连接 $ M'N $，交 $ AB $ 于点 $ O $。
4. 点 $ O $ 即为所求的位置。
[插图答案（和题干所给答案图一致即可）]

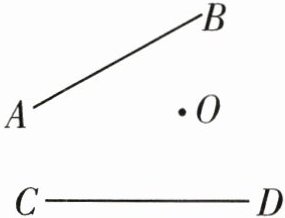
2. 李老师从湖中的小岛O处开始划船,先到AB岸,再到CD岸,最后返回小岛O,请画出最短路线。

答案：
2.
　
提示:首先画出点O关于直线AB的对称点G，同理，画出点O关于直线CD的对称点H，连接GH，交AB于点M，交CD于点N，从而可得GM=OM，NH=NO，所以GH=GM+MN+NH=OM+MN+NO。因为两点之间线段最短，所以线段GH最短，即线段OM、MN、NO的长度之和最短，即为最短路线。