第47页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
4. 推导探究 神奇的重复数。
【资料】由几个数字重复构成的多位数叫作“周期性重复数”,如123123123、6767等;“椅子数”是指0和1两个数字不断重复出现的数,数中的1看作椅子背,0看作座位,因此得名“椅子数”,如101、1001、10101等。
【计算】78×101=______ 56×101=______ 567×1001=______
【观察】

[左边对话框]我发现:一个两位数乘101,只要把这个两位数连续写(______)遍,得到的数就是它们的(______)。
[右边对话框]如果是三位数,就要乘(______),同样的方法也能得到这个三位数与(______)的(______)。
【结论】周期性重复数可以拆成一个数与(______)相乘的形式。
【运用】614×1001=(______) 3232=32×(______) 121121=121×(______) 47284728=4728×(______)
【资料】由几个数字重复构成的多位数叫作“周期性重复数”,如123123123、6767等;“椅子数”是指0和1两个数字不断重复出现的数,数中的1看作椅子背,0看作座位,因此得名“椅子数”,如101、1001、10101等。
【计算】78×101=______ 56×101=______ 567×1001=______
【观察】

[左边对话框]我发现:一个两位数乘101,只要把这个两位数连续写(______)遍,得到的数就是它们的(______)。
[右边对话框]如果是三位数,就要乘(______),同样的方法也能得到这个三位数与(______)的(______)。
【结论】周期性重复数可以拆成一个数与(______)相乘的形式。
【运用】614×1001=(______) 3232=32×(______) 121121=121×(______) 47284728=4728×(______)
答案:
4.【计算】7878 5656 567567
【观察】两积 1001 1001 积
【结论】椅子数
【运用】614614 101 1001 10001
提示:通过计算78×101=7878,56×101=5656,可以发现一个两位数乘101,只要把这个两位数连续写两遍得到的数就是它们的积。像101、1001这样的数,结合前面的计算,我们可以知道周期性重复数可以拆成一个数与椅子数相乘的形式。运用上述规律可知614×1001=614614,3232=32×101,121121=121×1001,47284728=4728×10001。
【观察】两积 1001 1001 积
【结论】椅子数
【运用】614614 101 1001 10001
提示:通过计算78×101=7878,56×101=5656,可以发现一个两位数乘101,只要把这个两位数连续写两遍得到的数就是它们的积。像101、1001这样的数,结合前面的计算,我们可以知道周期性重复数可以拆成一个数与椅子数相乘的形式。运用上述规律可知614×1001=614614,3232=32×101,121121=121×1001,47284728=4728×10001。
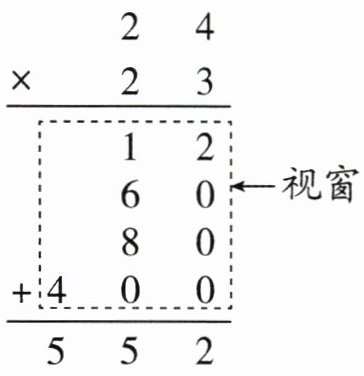
5. 算理理解 计算乘法的方法还有很多种,下面用2种方法计算了24×23,请用下面“画线”的方法计算132×23。
用“视窗”表记录心算结果
用“画线”也可以计算乘法
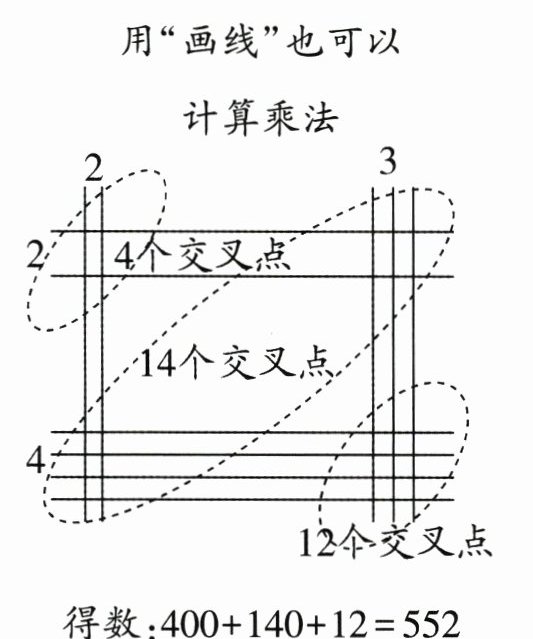
用“视窗”表记录心算结果

用“画线”也可以计算乘法

答案:
5.

132×23=2000+900+130+6=3036
提示:132从上往下画线,依次是百位、十位、个位,23从左往右画线,依次是十位、个位。
5.

132×23=2000+900+130+6=3036
提示:132从上往下画线,依次是百位、十位、个位,23从左往右画线,依次是十位、个位。
6. 模型意识 一只蚂蚁发现一块糖,它自己搬不动,便发信号唤来10只蚂蚁。可这些蚂蚁也搬不动,然后每只蚂蚁各自发信号唤来10只蚂蚁,结果仍然搬不动。于是蚂蚁们又各自发信号唤来10只蚂蚁,终于把糖搬回了洞里。一共有多少只蚂蚁来搬糖?
答案:
6. 方法一:第一次一只蚂蚁发信号后蚂蚁总数是1+10=11(只)
第二次11只蚂蚁发信号后蚂蚁总数是11+11×10=121(只)
第三次121只蚂蚁发信号后蚂蚁总数是121+121×10=1331(只)
方法二:1×11×11×11=1331(只)
提示:方法一:解决此题的关键是逐步计算出每次发信号唤来的蚂蚁只数,并且不要忘记加上每次发信号的蚂蚁只数。
方法二:因为1只蚂蚁唤来10只蚂蚁,蚂蚁的总数就变成了11只;11只蚂蚁又各自唤来10只蚂蚁,蚂蚁的总数就变成了11×(1+10)只……可见蚂蚁每唤来一次蚂蚁,蚂蚁的总数就扩大到原来的11倍。因为蚂蚁一共唤了3次,所以蚂蚁最后一共有1×11×11×11=1331(只)。
第二次11只蚂蚁发信号后蚂蚁总数是11+11×10=121(只)
第三次121只蚂蚁发信号后蚂蚁总数是121+121×10=1331(只)
方法二:1×11×11×11=1331(只)
提示:方法一:解决此题的关键是逐步计算出每次发信号唤来的蚂蚁只数,并且不要忘记加上每次发信号的蚂蚁只数。
方法二:因为1只蚂蚁唤来10只蚂蚁,蚂蚁的总数就变成了11只;11只蚂蚁又各自唤来10只蚂蚁,蚂蚁的总数就变成了11×(1+10)只……可见蚂蚁每唤来一次蚂蚁,蚂蚁的总数就扩大到原来的11倍。因为蚂蚁一共唤了3次,所以蚂蚁最后一共有1×11×11×11=1331(只)。
查看更多完整答案,请扫码查看


