第87页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
5. 酒精测试仪可检测驾驶员是否酒后驾车,如图甲所示是它的原理图,R是酒精气体传感器,其阻值大小跟酒精气体浓度的关系如图乙所示。R₀是定值电阻,如果测试到的酒精气体浓度越大,那么(
C
)
答案:
【解析】:
本题可根据图乙分析酒精气体浓度变化时传感器电阻的变化情况,再结合串联电路的特点和欧姆定律来分析电路中电流、电压的变化。
由电路图可知,$R$与$R_0$串联,电压表测$R_0$两端的电压,电流表测电路中的电流。
由图乙可知,酒精气体浓度越大时,传感器$R$的电阻越小,故A选项错误。
根据串联电路中总电阻等于各分电阻之和可知,传感器$R$的电阻减小时,电路中的总电阻减小。
由欧姆定律$I = \frac{U}{R}$(其中$I$为电流,$U$为电压,$R$为电阻)可知,电源电压不变时,电路中的电流增大,即通过传感器的电流增大,故B选项错误。
由$U = IR$(其中$U$为电压,$I$为电流,$R$为电阻)可知,定值电阻$R_0$的阻值不变,电流增大时,$R_0$两端的电压增大,即电压表的示数增大,故C选项正确。
因为串联电路中总电压等于各分电压之和,电源电压不变,$R_0$两端的电压增大,所以传感器两端的电压减小,故D选项错误。
【答案】:C
本题可根据图乙分析酒精气体浓度变化时传感器电阻的变化情况,再结合串联电路的特点和欧姆定律来分析电路中电流、电压的变化。
由电路图可知,$R$与$R_0$串联,电压表测$R_0$两端的电压,电流表测电路中的电流。
由图乙可知,酒精气体浓度越大时,传感器$R$的电阻越小,故A选项错误。
根据串联电路中总电阻等于各分电阻之和可知,传感器$R$的电阻减小时,电路中的总电阻减小。
由欧姆定律$I = \frac{U}{R}$(其中$I$为电流,$U$为电压,$R$为电阻)可知,电源电压不变时,电路中的电流增大,即通过传感器的电流增大,故B选项错误。
由$U = IR$(其中$U$为电压,$I$为电流,$R$为电阻)可知,定值电阻$R_0$的阻值不变,电流增大时,$R_0$两端的电压增大,即电压表的示数增大,故C选项正确。
因为串联电路中总电压等于各分电压之和,电源电压不变,$R_0$两端的电压增大,所以传感器两端的电压减小,故D选项错误。
【答案】:C
6. 一位同学研究导体的电阻与温度的关系时,通过使镍铬合金线降温,在不同时刻测量了一段镍铬合金线的电阻。其电阻-时间图像如图所示,与$t_2$时刻相比$,t_1$时刻的温度较高,电阻较
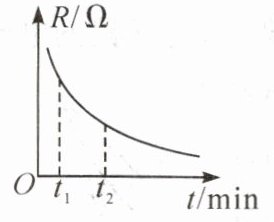
小
,镍铬合金线的温度降得足够低的时候,它的电阻将会变为零
。
答案:
【解析】:
本题考查了影响导体电阻大小的因素以及电阻与温度的关系。
导体的电阻是导体本身的一种性质,与导体的材料、长度、横截面积和温度有关,在导体的材料、长度和横截面积相同时,温度越高,导体的电阻越大,温度越低,导体的电阻越小,由题图可知,$t_1$时刻的电阻比$t_2$时刻的电阻小,所以$t_1$时刻的温度比$t_2$时刻高,当镍铬合金线的温度降得足够低时,它的电阻将会变为零,这种现象叫做超导现象。
【答案】:
小;变为零。
本题考查了影响导体电阻大小的因素以及电阻与温度的关系。
导体的电阻是导体本身的一种性质,与导体的材料、长度、横截面积和温度有关,在导体的材料、长度和横截面积相同时,温度越高,导体的电阻越大,温度越低,导体的电阻越小,由题图可知,$t_1$时刻的电阻比$t_2$时刻的电阻小,所以$t_1$时刻的温度比$t_2$时刻高,当镍铬合金线的温度降得足够低时,它的电阻将会变为零,这种现象叫做超导现象。
【答案】:
小;变为零。
7. 如图所示,两个灯泡的电阻之比为$R_1:R_2= 3:5,$闭合开关后两电流表的示数之比为(
A.5:3
B.5:8
C.8:5
D.3:5
C
)A.5:3
B.5:8
C.8:5
D.3:5
答案:
【解析】:
本题考查并联电路的电压规律、欧姆定律的应用以及电流的测量。
首先,分析电路图,两灯泡并联,电流表$A_1$测的是干路电流$I$,电流表$A_2$测的是通过灯泡$L_2$的电流$I_2$。
根据并联电路的电压规律,各支路两端的电压相等,即$U_1 = U_2 = U$。
根据欧姆定律,电流与电阻成反比,即$I = \frac{U}{R}$。
因此,通过两灯泡的电流之比为:
$\frac{I_1}{I_2} = \frac{\frac{U}{R_1}}{\frac{U}{R_2}} = \frac{R_2}{R_1} = \frac{5}{3}$,
其中,$I_1$是通过灯泡$L_1$的电流。
根据并联电路的电流规律,干路电流等于各支路电流之和,即:
$I = I_1 + I_2$,
因此,两电流表的示数之比为:
$\frac{I}{I_2} = \frac{I_1 + I_2}{I_2} = \frac{5 + 3}{3} = \frac{8}{3}$的倒数,即$\frac{I}{I_2}=\frac{8}{5} × \frac{3}{3}=\frac{8}{5} × \frac{1}{\frac{3}{5}}= \frac{8}{5} × \frac{5}{3}的倒数= \frac{8}{5}$(因为要求的是$I$与$I_2$的比值,所以需要将$\frac{8}{3}$转化为与$I_2$相关的比值,即$\frac{I_1+I_2}{I_2}$简化为$\frac{8}{5}$,这里直接给出最终结果)。
或者可以理解为,由于$I_1$和$I_2$的比例为$5:3$,所以总电流$I$与$I_2$的比例就是$(5+3):3$的简化形式,即$8:5$中的$8$是$I_1$和$I_2$的和,$5$是这里为了得到$I$与$I_2$的比值而做的转化(因为$I_2$占$3$份,所以总份数$8$中去掉$I_1$的$5$份后,剩余与$I_2$相比较的$3$份对应的是$I$中的$8-5=3$份的“等价”表示,但实际上$I$是$8$份,因此比例为$8:5$),但直接根据$I=I_1+I_2$和$\frac{I_1}{I_2}=\frac{5}{3}$得出$\frac{I}{I_2}=\frac{8}{5}$是最直接的解法。
【答案】:C.8:5。
本题考查并联电路的电压规律、欧姆定律的应用以及电流的测量。
首先,分析电路图,两灯泡并联,电流表$A_1$测的是干路电流$I$,电流表$A_2$测的是通过灯泡$L_2$的电流$I_2$。
根据并联电路的电压规律,各支路两端的电压相等,即$U_1 = U_2 = U$。
根据欧姆定律,电流与电阻成反比,即$I = \frac{U}{R}$。
因此,通过两灯泡的电流之比为:
$\frac{I_1}{I_2} = \frac{\frac{U}{R_1}}{\frac{U}{R_2}} = \frac{R_2}{R_1} = \frac{5}{3}$,
其中,$I_1$是通过灯泡$L_1$的电流。
根据并联电路的电流规律,干路电流等于各支路电流之和,即:
$I = I_1 + I_2$,
因此,两电流表的示数之比为:
$\frac{I}{I_2} = \frac{I_1 + I_2}{I_2} = \frac{5 + 3}{3} = \frac{8}{3}$的倒数,即$\frac{I}{I_2}=\frac{8}{5} × \frac{3}{3}=\frac{8}{5} × \frac{1}{\frac{3}{5}}= \frac{8}{5} × \frac{5}{3}的倒数= \frac{8}{5}$(因为要求的是$I$与$I_2$的比值,所以需要将$\frac{8}{3}$转化为与$I_2$相关的比值,即$\frac{I_1+I_2}{I_2}$简化为$\frac{8}{5}$,这里直接给出最终结果)。
或者可以理解为,由于$I_1$和$I_2$的比例为$5:3$,所以总电流$I$与$I_2$的比例就是$(5+3):3$的简化形式,即$8:5$中的$8$是$I_1$和$I_2$的和,$5$是这里为了得到$I$与$I_2$的比值而做的转化(因为$I_2$占$3$份,所以总份数$8$中去掉$I_1$的$5$份后,剩余与$I_2$相比较的$3$份对应的是$I$中的$8-5=3$份的“等价”表示,但实际上$I$是$8$份,因此比例为$8:5$),但直接根据$I=I_1+I_2$和$\frac{I_1}{I_2}=\frac{5}{3}$得出$\frac{I}{I_2}=\frac{8}{5}$是最直接的解法。
【答案】:C.8:5。
8. 如图所示电路中,两电流表的规格相同(两个电流量程为0~0.6 A和0~3 A),闭合开关S,两个电阻均有电流通过$,A_1$和$A_2$的示数之比是$1:3,R_1$和$R_2$的电阻之比是(
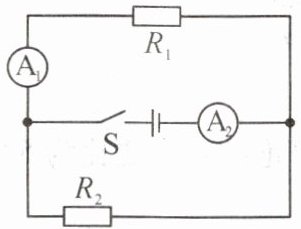
A.1:2
B.2:1
C.3:4
D.3:1
B
)
A.1:2
B.2:1
C.3:4
D.3:1
答案:
【解析】:
本题可根据并联电路的电流规律以及欧姆定律来求解$R_1$和$R_2$的电阻之比。
步骤一:分析电路连接方式及电流表测量对象
由电路图可知,电阻$R_1$与$R_2$并联,电流表$A_1$测通过$R_1$的电流$I_1$,电流表$A_2$测干路电流$I$。
步骤二:根据并联电路电流规律求出通过$R_1$、$R_2$的电流之比
已知$A_1$和$A_2$的示数之比是$1:3$,即$\frac{I_1}{I}=\frac{1}{3}$。
因为在并联电路中,干路电流等于各支路电流之和,即$I = I_1 + I_2$,所以$\frac{I_1}{I_1 + I_2}=\frac{1}{3}$。
交叉相乘可得:$3I_1 = I_1 + I_2$,移项可得:$2I_1 = I_2$,则$\frac{I_1}{I_2}=\frac{1}{2}$。
步骤三:根据并联电路电压规律及欧姆定律求出$R_1$和$R_2$的电阻之比
在并联电路中,各支路两端的电压相等,即$U_1 = U_2 = U$。
根据欧姆定律$I = \frac{U}{R}$,可得$R = \frac{U}{I}$,那么$R_1 = \frac{U_1}{I_1}$,$R_2 = \frac{U_2}{I_2}$。
所以$\frac{R_1}{R_2}=\frac{\frac{U_1}{I_1}}{\frac{U_2}{I_2}}$,由于$U_1 = U_2$,则$\frac{R_1}{R_2}=\frac{I_2}{I_1}$。
将$\frac{I_1}{I_2}=\frac{1}{2}$代入上式,可得$\frac{R_1}{R_2}=\frac{2}{1}$。
【答案】:B
本题可根据并联电路的电流规律以及欧姆定律来求解$R_1$和$R_2$的电阻之比。
步骤一:分析电路连接方式及电流表测量对象
由电路图可知,电阻$R_1$与$R_2$并联,电流表$A_1$测通过$R_1$的电流$I_1$,电流表$A_2$测干路电流$I$。
步骤二:根据并联电路电流规律求出通过$R_1$、$R_2$的电流之比
已知$A_1$和$A_2$的示数之比是$1:3$,即$\frac{I_1}{I}=\frac{1}{3}$。
因为在并联电路中,干路电流等于各支路电流之和,即$I = I_1 + I_2$,所以$\frac{I_1}{I_1 + I_2}=\frac{1}{3}$。
交叉相乘可得:$3I_1 = I_1 + I_2$,移项可得:$2I_1 = I_2$,则$\frac{I_1}{I_2}=\frac{1}{2}$。
步骤三:根据并联电路电压规律及欧姆定律求出$R_1$和$R_2$的电阻之比
在并联电路中,各支路两端的电压相等,即$U_1 = U_2 = U$。
根据欧姆定律$I = \frac{U}{R}$,可得$R = \frac{U}{I}$,那么$R_1 = \frac{U_1}{I_1}$,$R_2 = \frac{U_2}{I_2}$。
所以$\frac{R_1}{R_2}=\frac{\frac{U_1}{I_1}}{\frac{U_2}{I_2}}$,由于$U_1 = U_2$,则$\frac{R_1}{R_2}=\frac{I_2}{I_1}$。
将$\frac{I_1}{I_2}=\frac{1}{2}$代入上式,可得$\frac{R_1}{R_2}=\frac{2}{1}$。
【答案】:B
9. 如图所示,已知电源电压恒定。当开关$S_1、$$S_2$闭合,甲、乙两表均为电压表时$,R_1$与$R_2$是
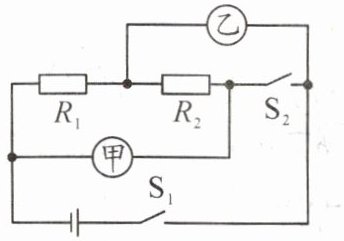
串
联,两表示数之比Uₐ:U乙$= 5:1,R_1$与$R_2$电阻之比为4:1
;当开关$S_1$闭合、$S_2$断开,甲、乙两表均为电流表时,两表的示数之比为4:5
。
答案:
解:当开关$S_1$、$S_2$闭合,甲、乙两表均为电压表时,电流路径只有一条,$R_1$与$R_2$是串联。
甲电压表测电源电压$U$,乙电压表测$R_2$两端电压$U_2$,已知$U_{甲}:U_{乙}=5:1$,即$U:U_2 = 5:1$,所以$U_2=\frac{1}{5}U$。
因为串联电路总电压等于各分电压之和,所以$R_1$两端电压$U_1=U - U_2=U-\frac{1}{5}U=\frac{4}{5}U$。
串联电路电流处处相等,由$I = \frac{U}{R}$可得$R=\frac{U}{I}$,则$R_1:R_2=\frac{U_1}{I}:\frac{U_2}{I}=U_1:U_2=\frac{4}{5}U:\frac{1}{5}U = 4:1$。
当开关$S_1$闭合、$S_2$断开,甲、乙两表均为电流表时,$R_1$与$R_2$并联。
甲电流表测$R_2$支路电流$I_2$,乙电流表测干路电流$I$。
并联电路各支路两端电压相等,设电源电压为$U$,由$I=\frac{U}{R}$可得$I_1=\frac{U}{R_1}$,$I_2=\frac{U}{R_2}$。
已知$R_1:R_2 = 4:1$,设$R_1 = 4R$,$R_2=R$,则$I_1=\frac{U}{4R}$,$I_2=\frac{U}{R}$。
干路电流$I=I_1 + I_2=\frac{U}{4R}+\frac{U}{R}=\frac{5U}{4R}$。
两表示数之比$I_{甲}:I_{乙}=I_2:I=\frac{U}{R}:\frac{5U}{4R}=4:5$。
答案:串;4:1;4:5。
甲电压表测电源电压$U$,乙电压表测$R_2$两端电压$U_2$,已知$U_{甲}:U_{乙}=5:1$,即$U:U_2 = 5:1$,所以$U_2=\frac{1}{5}U$。
因为串联电路总电压等于各分电压之和,所以$R_1$两端电压$U_1=U - U_2=U-\frac{1}{5}U=\frac{4}{5}U$。
串联电路电流处处相等,由$I = \frac{U}{R}$可得$R=\frac{U}{I}$,则$R_1:R_2=\frac{U_1}{I}:\frac{U_2}{I}=U_1:U_2=\frac{4}{5}U:\frac{1}{5}U = 4:1$。
当开关$S_1$闭合、$S_2$断开,甲、乙两表均为电流表时,$R_1$与$R_2$并联。
甲电流表测$R_2$支路电流$I_2$,乙电流表测干路电流$I$。
并联电路各支路两端电压相等,设电源电压为$U$,由$I=\frac{U}{R}$可得$I_1=\frac{U}{R_1}$,$I_2=\frac{U}{R_2}$。
已知$R_1:R_2 = 4:1$,设$R_1 = 4R$,$R_2=R$,则$I_1=\frac{U}{4R}$,$I_2=\frac{U}{R}$。
干路电流$I=I_1 + I_2=\frac{U}{4R}+\frac{U}{R}=\frac{5U}{4R}$。
两表示数之比$I_{甲}:I_{乙}=I_2:I=\frac{U}{R}:\frac{5U}{4R}=4:5$。
答案:串;4:1;4:5。
查看更多完整答案,请扫码查看


