第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
1. 如图所示,用完全相同的两个滑轮组,分别将重为$G_{1}$、$G_{2}$的两个物体匀速提升相同的高度,若$G_{1}>G_{2}$,提升重物所做的有用功分别为$W_{1}$、$W_{2}$,机械效率分别为$\eta_{1}$、$\eta_{2}$,则下列判断正确的是( )

A.$W_{1}>W_{2}$ $\eta_{1}>\eta_{2}$
B.$W_{1}>W_{2}$ $\eta_{1}= \eta_{2}$
C.$W_{1}= W_{2}$ $\eta_{1}<\eta_{2}$
D.$W_{1}= W_{2}$ $\eta_{1}>\eta_{2}$
A

A.$W_{1}>W_{2}$ $\eta_{1}>\eta_{2}$
B.$W_{1}>W_{2}$ $\eta_{1}= \eta_{2}$
C.$W_{1}= W_{2}$ $\eta_{1}<\eta_{2}$
D.$W_{1}= W_{2}$ $\eta_{1}>\eta_{2}$
答案:
【解析】:
本题可根据有用功和机械效率的计算公式,结合已知条件分别分析有用功和机械效率的大小关系。
有用功的计算公式为$W_{有}=Gh$($G$是物体重力,$h$是物体上升高度),机械效率的计算公式为$\eta=\frac{W_{有}}{W_{总}}×100\%=\frac{W_{有}}{W_{有}+W_{额}}×100\%$。
分析有用功大小关系:
已知两个滑轮组将重为$G_{1}$、$G_{2}$的两个物体匀速提升相同的高度$h$,根据有用功公式$W_{有}=Gh$,可得$W_{1}=G_{1}h$,$W_{2}=G_{2}h$。
因为$G_{1}>G_{2}$,$h$相同,所以$G_{1}h>G_{2}h$,即$W_{1}>W_{2}$。
分析机械效率大小关系:
由图可知,两滑轮组完全相同,将重物提升相同高度,所以额外功$W_{额}$相同(额外功主要是克服动滑轮重力等做的功,动滑轮相同,提升高度相同,额外功就相同)。
根据机械效率公式$\eta=\frac{W_{有}}{W_{有}+W_{额}}×100\%=\frac{1}{1 + \frac{W_{额}}{W_{有}}}×100\%$,因为$W_{1}>W_{2}$,即$W_{有1}>W_{有2}$,在$W_{额}$相同的情况下,$W_{有}$越大,$\frac{W_{额}}{W_{有}}$越小,$1 + \frac{W_{额}}{W_{有}}$越小,$\frac{1}{1 + \frac{W_{额}}{W_{有}}}$越大,机械效率$\eta$越高。
所以$\eta_{1}>\eta_{2}$。
【答案】:A。
本题可根据有用功和机械效率的计算公式,结合已知条件分别分析有用功和机械效率的大小关系。
有用功的计算公式为$W_{有}=Gh$($G$是物体重力,$h$是物体上升高度),机械效率的计算公式为$\eta=\frac{W_{有}}{W_{总}}×100\%=\frac{W_{有}}{W_{有}+W_{额}}×100\%$。
分析有用功大小关系:
已知两个滑轮组将重为$G_{1}$、$G_{2}$的两个物体匀速提升相同的高度$h$,根据有用功公式$W_{有}=Gh$,可得$W_{1}=G_{1}h$,$W_{2}=G_{2}h$。
因为$G_{1}>G_{2}$,$h$相同,所以$G_{1}h>G_{2}h$,即$W_{1}>W_{2}$。
分析机械效率大小关系:
由图可知,两滑轮组完全相同,将重物提升相同高度,所以额外功$W_{额}$相同(额外功主要是克服动滑轮重力等做的功,动滑轮相同,提升高度相同,额外功就相同)。
根据机械效率公式$\eta=\frac{W_{有}}{W_{有}+W_{额}}×100\%=\frac{1}{1 + \frac{W_{额}}{W_{有}}}×100\%$,因为$W_{1}>W_{2}$,即$W_{有1}>W_{有2}$,在$W_{额}$相同的情况下,$W_{有}$越大,$\frac{W_{额}}{W_{有}}$越小,$1 + \frac{W_{额}}{W_{有}}$越小,$\frac{1}{1 + \frac{W_{额}}{W_{有}}}$越大,机械效率$\eta$越高。
所以$\eta_{1}>\eta_{2}$。
【答案】:A。
2. 如图所示,利用滑轮组在4s内将一重为9N的物体匀速向上提升了10cm,拉力为4N,不计一切摩擦和绳重($g$取10N/kg)。下列说法正确的是(
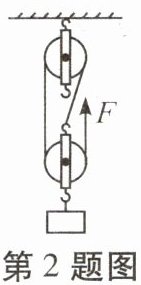
A.动滑轮重力为5N
B.滑轮组的机械效率为75%
C.拉力所做的功为0.4J
D.拉力的功率为0.4W
B
) 
A.动滑轮重力为5N
B.滑轮组的机械效率为75%
C.拉力所做的功为0.4J
D.拉力的功率为0.4W
答案:
【解析】:
本题考查了滑轮组的相关计算以及机械效率的计算。
选项A:由图可知$n=3$,不计一切摩擦和绳重,由$F=\frac{1}{n}(G+G_{动})$可得动滑轮的重力$G_{动}=nF-G=3×4N-9N=3N$,故A错误。
选项B:滑轮组的机械效率$\eta=\frac{W_{有}}{W_{总}}×100\%=\frac{Gh}{Fs}×100\%=\frac{Gh}{Fnh}×100\%=\frac{G}{nF}×100\%=\frac{9N}{3×4N}×100\%=75\%$,故B正确。
选项C:拉力所做的功$W_{总}=Fs=Fnh=4N×3×0.1m=1.2J$,故C错误。
选项D:拉力的功率$P=\frac{W_{总}}{t}=\frac{1.2J}{4s}=0.3W$,故D错误。
【答案】:B。
本题考查了滑轮组的相关计算以及机械效率的计算。
选项A:由图可知$n=3$,不计一切摩擦和绳重,由$F=\frac{1}{n}(G+G_{动})$可得动滑轮的重力$G_{动}=nF-G=3×4N-9N=3N$,故A错误。
选项B:滑轮组的机械效率$\eta=\frac{W_{有}}{W_{总}}×100\%=\frac{Gh}{Fs}×100\%=\frac{Gh}{Fnh}×100\%=\frac{G}{nF}×100\%=\frac{9N}{3×4N}×100\%=75\%$,故B正确。
选项C:拉力所做的功$W_{总}=Fs=Fnh=4N×3×0.1m=1.2J$,故C错误。
选项D:拉力的功率$P=\frac{W_{总}}{t}=\frac{1.2J}{4s}=0.3W$,故D错误。
【答案】:B。
3. 小明同学用如图所示的滑轮组提升重物。下列说法中不能提高滑轮组的机械效率的方法是(

A.增大物体的重力$G$
B.增大物体被提升的高度$h$
C.使用轻质的动滑轮
D.在滑轮的轮轴处涂润滑剂
B
) 
A.增大物体的重力$G$
B.增大物体被提升的高度$h$
C.使用轻质的动滑轮
D.在滑轮的轮轴处涂润滑剂
答案:
【解析】:
本题可根据滑轮组机械效率的相关知识,分析每个选项对滑轮组机械效率的影响。
滑轮组的机械效率公式为$\eta=\frac{W_{有}}{W_{总}}=\frac{Gh}{Fs}$(其中$G$是物体重力,$h$是物体上升高度,$F$是拉力,$s$是绳子自由端移动距离),也可表示为$\eta=\frac{W_{有}}{W_{有}+W_{额}}$($W_{额}$为额外功)。
选项A:增大物体的重力$G$
在额外功一定的情况下,根据$W_{有}=Gh$,增大物体的重力$G$,有用功$W_{有}$会增大,由$\eta=\frac{W_{有}}{W_{有}+W_{额}}$可知,有用功增大,额外功不变,机械效率$\eta$会提高,所以该选项不符合题意。
选项B:增大物体被提升的高度$h$
根据滑轮组机械效率公式$\eta=\frac{W_{有}}{W_{总}}=\frac{Gh}{Fs}$,在不考虑绳重和摩擦时,$F = \frac{1}{n}(G + G_{动})$($n$为承担物重的绳子段数,$G_{动}$为动滑轮重力),$s = nh$,则$\eta=\frac{Gh}{\frac{1}{n}(G + G_{动})× nh}=\frac{G}{G + G_{动}}$,可以看出滑轮组的机械效率与物体被提升的高度$h$无关,所以增大物体被提升的高度$h$不能提高滑轮组的机械效率,该选项符合题意。
选项C:使用轻质的动滑轮
使用轻质的动滑轮,动滑轮的重力$G_{动}$减小,在有用功一定的情况下,额外功$W_{额}=G_{动}h$会减小,由$\eta=\frac{W_{有}}{W_{有}+W_{额}}$可知,有用功不变,额外功减小,机械效率$\eta$会提高,所以该选项不符合题意。
选项D:在滑轮的轮轴处涂润滑剂
在滑轮的轮轴处涂润滑剂,可以减小摩擦,从而减小额外功,在有用功一定的情况下,由$\eta=\frac{W_{有}}{W_{有}+W_{额}}$可知,有用功不变,额外功减小,机械效率$\eta$会提高,所以该选项不符合题意。
【答案】:B
本题可根据滑轮组机械效率的相关知识,分析每个选项对滑轮组机械效率的影响。
滑轮组的机械效率公式为$\eta=\frac{W_{有}}{W_{总}}=\frac{Gh}{Fs}$(其中$G$是物体重力,$h$是物体上升高度,$F$是拉力,$s$是绳子自由端移动距离),也可表示为$\eta=\frac{W_{有}}{W_{有}+W_{额}}$($W_{额}$为额外功)。
选项A:增大物体的重力$G$
在额外功一定的情况下,根据$W_{有}=Gh$,增大物体的重力$G$,有用功$W_{有}$会增大,由$\eta=\frac{W_{有}}{W_{有}+W_{额}}$可知,有用功增大,额外功不变,机械效率$\eta$会提高,所以该选项不符合题意。
选项B:增大物体被提升的高度$h$
根据滑轮组机械效率公式$\eta=\frac{W_{有}}{W_{总}}=\frac{Gh}{Fs}$,在不考虑绳重和摩擦时,$F = \frac{1}{n}(G + G_{动})$($n$为承担物重的绳子段数,$G_{动}$为动滑轮重力),$s = nh$,则$\eta=\frac{Gh}{\frac{1}{n}(G + G_{动})× nh}=\frac{G}{G + G_{动}}$,可以看出滑轮组的机械效率与物体被提升的高度$h$无关,所以增大物体被提升的高度$h$不能提高滑轮组的机械效率,该选项符合题意。
选项C:使用轻质的动滑轮
使用轻质的动滑轮,动滑轮的重力$G_{动}$减小,在有用功一定的情况下,额外功$W_{额}=G_{动}h$会减小,由$\eta=\frac{W_{有}}{W_{有}+W_{额}}$可知,有用功不变,额外功减小,机械效率$\eta$会提高,所以该选项不符合题意。
选项D:在滑轮的轮轴处涂润滑剂
在滑轮的轮轴处涂润滑剂,可以减小摩擦,从而减小额外功,在有用功一定的情况下,由$\eta=\frac{W_{有}}{W_{有}+W_{额}}$可知,有用功不变,额外功减小,机械效率$\eta$会提高,所以该选项不符合题意。
【答案】:B
4. 如图所示,在不计绳重和摩擦的情况下,用动滑轮把重40N的物体匀速提高2m,所用的拉力为25N,则拉力做功是

100
J,动滑轮的机械效率是80
%;如果将重物增加至100N,匀速提升相同高度,则这个动滑轮的机械效率将变大
(选填“变大”“变小”或“不变”)。
答案:
解:
1. 由图可知,动滑轮绳子段数$n=2$,拉力移动距离$s=nh=2×2m=4m$,拉力做功$W_{总}=Fs=25N×4m=100J$。
2. 有用功$W_{有}=Gh=40N×2m=80J$,机械效率$\eta=\frac{W_{有}}{W_{总}}×100\%=\frac{80J}{100J}×100\%=80\%$。
3. 变大。
答案:100;80;变大。
1. 由图可知,动滑轮绳子段数$n=2$,拉力移动距离$s=nh=2×2m=4m$,拉力做功$W_{总}=Fs=25N×4m=100J$。
2. 有用功$W_{有}=Gh=40N×2m=80J$,机械效率$\eta=\frac{W_{有}}{W_{总}}×100\%=\frac{80J}{100J}×100\%=80\%$。
3. 变大。
答案:100;80;变大。
5. 在“测滑轮组机械效率”实验中,物体重为6N。若物体上升高度为10cm,此时弹簧测力计的示数如图所示,则拉力做的有用功是
0.6
J,滑轮组的机械效率是83.3
%。若仅增加物体的质量,该滑轮组的机械效率将增大
(选填“增大”“减小”或“不变”)。(不计绳重及摩擦)
答案:
【解析】:
本题主要考查了滑轮组机械效率的计算以及影响滑轮组机械效率的因素。
首先,我们需要计算拉力做的有用功。有用功是物体被提升所做的功,计算公式为$W_{有用} = Gh$,其中$G$是物体的重力,$h$是物体上升的高度。
接着,我们需要计算滑轮组的机械效率。机械效率是有用功与总功的比值,计算公式为$\eta = \frac{W_{有用}}{W_{总}} × 100\%$。由于题目中给出了弹簧测力计的示数,我们可以通过读图得知拉力的大小,然后计算拉力做的总功$W_{总} = Fs$,其中$F$是拉力,$s$是拉力作用点移动的距离。在本题中,由于滑轮组的关系,拉力作用点移动的距离是物体上升高度的三倍,即$s = 3h$。
最后,我们需要分析仅增加物体的质量时,滑轮组的机械效率将如何变化。这需要我们理解滑轮组机械效率的影响因素,特别是物重对机械效率的影响。
【答案】:
有用功的计算:
$W_{有用} = Gh = 6 × 0.1 = 0.6J$
拉力的读数:
由图可知,弹簧测力计的分度值为$0.2N$,指针指在$2N$下面第$4$个小格处,所以拉力$F = 2.4N$(或$2.40N$,由于读数会有一定误差,所以$2.4N$和$2.40N$均可);
拉力作用点移动的距离:
$s = 3h = 3 × 0.1 = 0.3m$
拉力做的总功:
$W_{总} = Fs = 2.4 × 0.3 = 0.72J$
滑轮组的机械效率:
$\eta = \frac{W_{有用}}{W_{总}} × 100\% = \frac{0.6}{0.72} × 100\% \approx 83.3\%$
仅增加物体的质量时,由于物重增大,滑轮组做的有用功增多,额外功不变(不计绳重及摩擦),所以有用功在总功中所占的比例增大,即滑轮组的机械效率增大。
综上,答案为:$0.6$;$83.3$;增大。
本题主要考查了滑轮组机械效率的计算以及影响滑轮组机械效率的因素。
首先,我们需要计算拉力做的有用功。有用功是物体被提升所做的功,计算公式为$W_{有用} = Gh$,其中$G$是物体的重力,$h$是物体上升的高度。
接着,我们需要计算滑轮组的机械效率。机械效率是有用功与总功的比值,计算公式为$\eta = \frac{W_{有用}}{W_{总}} × 100\%$。由于题目中给出了弹簧测力计的示数,我们可以通过读图得知拉力的大小,然后计算拉力做的总功$W_{总} = Fs$,其中$F$是拉力,$s$是拉力作用点移动的距离。在本题中,由于滑轮组的关系,拉力作用点移动的距离是物体上升高度的三倍,即$s = 3h$。
最后,我们需要分析仅增加物体的质量时,滑轮组的机械效率将如何变化。这需要我们理解滑轮组机械效率的影响因素,特别是物重对机械效率的影响。
【答案】:
有用功的计算:
$W_{有用} = Gh = 6 × 0.1 = 0.6J$
拉力的读数:
由图可知,弹簧测力计的分度值为$0.2N$,指针指在$2N$下面第$4$个小格处,所以拉力$F = 2.4N$(或$2.40N$,由于读数会有一定误差,所以$2.4N$和$2.40N$均可);
拉力作用点移动的距离:
$s = 3h = 3 × 0.1 = 0.3m$
拉力做的总功:
$W_{总} = Fs = 2.4 × 0.3 = 0.72J$
滑轮组的机械效率:
$\eta = \frac{W_{有用}}{W_{总}} × 100\% = \frac{0.6}{0.72} × 100\% \approx 83.3\%$
仅增加物体的质量时,由于物重增大,滑轮组做的有用功增多,额外功不变(不计绳重及摩擦),所以有用功在总功中所占的比例增大,即滑轮组的机械效率增大。
综上,答案为:$0.6$;$83.3$;增大。
6. 如图所示,斜面长$s= 1.2m$、高$h= 0.3m$,现将重为16N的物体沿斜面向上从底端匀速拉到顶端,若拉力$F= 5N$,拉力的功率为3W,则(

A.斜面的机械效率为75%
B.拉力做的总功为4.8J
C.物体沿斜面的运动速度是0.6m/s
D.物体在斜面上受到的摩擦力是5N
C
) 
A.斜面的机械效率为75%
B.拉力做的总功为4.8J
C.物体沿斜面的运动速度是0.6m/s
D.物体在斜面上受到的摩擦力是5N
答案:
【解析】:
本题主要考查斜面的机械效率、总功、速度以及摩擦力的计算,需要用到机械效率公式、功的公式、功率公式以及力的平衡条件。
A选项,计算斜面的机械效率。
斜面的机械效率$\eta$定义为有用功$W_{有}$与总功$W_{总}$的比值,即$\eta = \frac{W_{有}}{W_{总}} × 100\%$。
有用功$W_{有}$是物体被提升所做的功,即$W_{有} = Gh = 16 × 0.3 = 4.8J$($G$为物体重力,$h$为斜面高度)。
总功$W_{总}$是拉力所做的功,即$W_{总} = Fs = 5 × 1.2 = 6J$($F$为拉力,$s$为斜面长度)。
所以,斜面的机械效率$\eta = \frac{4.8}{6} × 100\% = 80\%$,与A选项中的$75\%$不符,所以A选项错误。
B选项,由A选项分析可知,拉力做的总功为$6J$,与B选项中的$4.8J$不符,所以B选项错误。
C选项,计算物体沿斜面的运动速度。
已知拉力的功率为$3W$,由功率公式$P = Fv$($P$为功率,$F$为拉力,$v$为速度)可得,物体沿斜面的运动速度$v = \frac{P}{F} = \frac{3}{5} = 0.6m/s$,与C选项中的$0.6m/s$相符,所以C选项正确。
D选项,计算物体在斜面上受到的摩擦力。
在斜面上,物体受到的力有重力、拉力、支持力和摩擦力。由于物体是匀速运动的,所以这些力是平衡的。
特别地,沿斜面方向,拉力$F$等于重力沿斜面的分力与摩擦力$f$之和,即$F = \frac{Gh}{s} + f$。
解这个方程,得到摩擦力$f = F - \frac{Gh}{s} = 5 - \frac{16 × 0.3}{1.2} = 1N$,与D选项中的$5N$不符,所以D选项错误。
【答案】:C
本题主要考查斜面的机械效率、总功、速度以及摩擦力的计算,需要用到机械效率公式、功的公式、功率公式以及力的平衡条件。
A选项,计算斜面的机械效率。
斜面的机械效率$\eta$定义为有用功$W_{有}$与总功$W_{总}$的比值,即$\eta = \frac{W_{有}}{W_{总}} × 100\%$。
有用功$W_{有}$是物体被提升所做的功,即$W_{有} = Gh = 16 × 0.3 = 4.8J$($G$为物体重力,$h$为斜面高度)。
总功$W_{总}$是拉力所做的功,即$W_{总} = Fs = 5 × 1.2 = 6J$($F$为拉力,$s$为斜面长度)。
所以,斜面的机械效率$\eta = \frac{4.8}{6} × 100\% = 80\%$,与A选项中的$75\%$不符,所以A选项错误。
B选项,由A选项分析可知,拉力做的总功为$6J$,与B选项中的$4.8J$不符,所以B选项错误。
C选项,计算物体沿斜面的运动速度。
已知拉力的功率为$3W$,由功率公式$P = Fv$($P$为功率,$F$为拉力,$v$为速度)可得,物体沿斜面的运动速度$v = \frac{P}{F} = \frac{3}{5} = 0.6m/s$,与C选项中的$0.6m/s$相符,所以C选项正确。
D选项,计算物体在斜面上受到的摩擦力。
在斜面上,物体受到的力有重力、拉力、支持力和摩擦力。由于物体是匀速运动的,所以这些力是平衡的。
特别地,沿斜面方向,拉力$F$等于重力沿斜面的分力与摩擦力$f$之和,即$F = \frac{Gh}{s} + f$。
解这个方程,得到摩擦力$f = F - \frac{Gh}{s} = 5 - \frac{16 × 0.3}{1.2} = 1N$,与D选项中的$5N$不符,所以D选项错误。
【答案】:C
7. 如图所示,斜面长5m,高2m。用平行于斜面$F= 40N$的拉力,将重90N的物体,从斜面底端匀速拉到顶端。在此过程中,下列说法正确的是(

A.此装置不可以省力
B.该斜面机械效率为90%
C.物体受到的摩擦力为5N
D.对物体做的有用功为200J
B
) 
A.此装置不可以省力
B.该斜面机械效率为90%
C.物体受到的摩擦力为5N
D.对物体做的有用功为200J
答案:
【解析】:
本题主要考查简单机械中斜面的应用,包括省力情况、有用功、总功、额外功以及机械效率的计算,同时涉及摩擦力的求解。
A选项分析:使用斜面的目的是为了省力,从题目中可知拉力$F = 40N$,物体重$G = 90N$,$F\lt G$,说明此装置可以省力,A选项错误。
B选项分析:
有用功是克服物体重力所做的功,根据公式$W_{有}=Gh$,其中$G = 90N$,$h = 2m$,可得$W_{有}=90N×2m = 180J$。
总功是拉力$F$所做的功,根据公式$W_{总}=Fs$,其中$F = 40N$,$s = 5m$,可得$W_{总}=40N×5m = 200J$。
根据机械效率公式$\eta=\frac{W_{有}}{W_{总}}×100\%$,将$W_{有}=180J$,$W_{总}=200J$代入可得$\eta=\frac{180J}{200J}×100\% = 90\%$,B选项正确。
C选项分析:
额外功$W_{额}=W_{总}-W_{有}$,将$W_{有}=180J$,$W_{总}=200J$代入可得$W_{额}=200J - 180J = 20J$。
因为额外功是克服摩擦力做的功,根据公式$W_{额}=fs$,可得摩擦力$f=\frac{W_{额}}{s}$,将$W_{额}=20J$,$s = 5m$代入可得$f=\frac{20J}{5m}=4N$,C选项错误。
D选项分析:
由前面计算可知,有用功$W_{有}=Gh = 90N×2m = 180J$,D选项错误。
【答案】:B
本题主要考查简单机械中斜面的应用,包括省力情况、有用功、总功、额外功以及机械效率的计算,同时涉及摩擦力的求解。
A选项分析:使用斜面的目的是为了省力,从题目中可知拉力$F = 40N$,物体重$G = 90N$,$F\lt G$,说明此装置可以省力,A选项错误。
B选项分析:
有用功是克服物体重力所做的功,根据公式$W_{有}=Gh$,其中$G = 90N$,$h = 2m$,可得$W_{有}=90N×2m = 180J$。
总功是拉力$F$所做的功,根据公式$W_{总}=Fs$,其中$F = 40N$,$s = 5m$,可得$W_{总}=40N×5m = 200J$。
根据机械效率公式$\eta=\frac{W_{有}}{W_{总}}×100\%$,将$W_{有}=180J$,$W_{总}=200J$代入可得$\eta=\frac{180J}{200J}×100\% = 90\%$,B选项正确。
C选项分析:
额外功$W_{额}=W_{总}-W_{有}$,将$W_{有}=180J$,$W_{总}=200J$代入可得$W_{额}=200J - 180J = 20J$。
因为额外功是克服摩擦力做的功,根据公式$W_{额}=fs$,可得摩擦力$f=\frac{W_{额}}{s}$,将$W_{额}=20J$,$s = 5m$代入可得$f=\frac{20J}{5m}=4N$,C选项错误。
D选项分析:
由前面计算可知,有用功$W_{有}=Gh = 90N×2m = 180J$,D选项错误。
【答案】:B
查看更多完整答案,请扫码查看


