《2025年零障碍导教导学案九年级物理全一册沪粤版》

8. 如图所示是女子攀岩大赛的比赛情景,当两位选手都登顶后,体重越大的选手做功越多(选填“多”或“少”)；最先登上峰顶的选手做功可能(选填“一定”或“可能”)最快。

答案： 【解析】：
本题可根据功的计算公式$W = Gh$（其中$W$是功，$G$是重力，$h$是在重力方向上移动的距离）以及功率的概念来进行分析。
分析体重越大的选手做功情况：
两位选手都登顶，即她们在重力方向上移动的距离$h$相同。根据重力公式$G=mg$（其中$m$是质量，$g$是重力加速度），体重越大，质量$m$越大，重力$G$就越大。再根据功的计算公式$W = Gh$，在$h$相同的情况下，$G$越大，做功$W$越多。
分析最先登上峰顶的选手做功快慢情况：
功率是表示做功快慢的物理量，其计算公式为$P=\frac{W}{t}$（其中$P$是功率，$W$是功，$t$是时间）。最先登上峰顶的选手，所用时间$t$最短，但做功$W$的多少还与选手的体重有关。如果体重较小的选手虽然用时稍长，但做功少很多，那么有可能体重较小选手的功率更大，即做功不一定最快，所以最先登上峰顶的选手做功可能最快。
【答案】：
多；可能

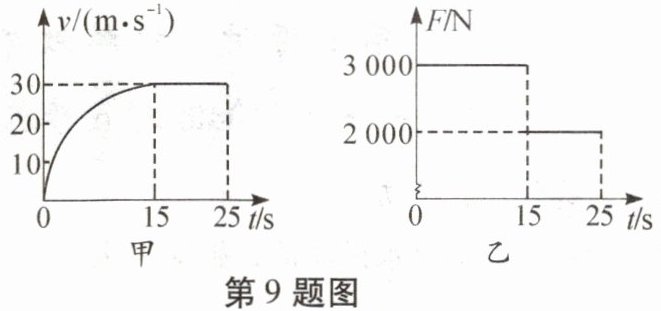
9. 如图甲所示,某轿车在水平地面上行驶,25 s的时间内其v-t和F-t的图像分别如图甲、乙所示。已知前15 s轿车运动的路程为180 m,则整个过程汽车发动机做的功1.14×10⁶J,汽车匀速运动阶段发动机的功率为60kW。

答案： 解：
1. 0-15s内：
W₁=F₁s₁=3000N×180m=5.4×10⁵J
2. 15-25s内：
t₂=25s-15s=10s，v₂=30m/s
s₂=v₂t₂=30m/s×10s=300m
W₂=F₂s₂=2000N×300m=6×10⁵J
3. 整个过程做功：
W=W₁+W₂=5.4×10⁵J+6×10⁵J=1.14×10⁶J
4. 匀速阶段功率：
P=F₂v₂=2000N×30m/s=60000W=60kW
1.14×10⁶；60

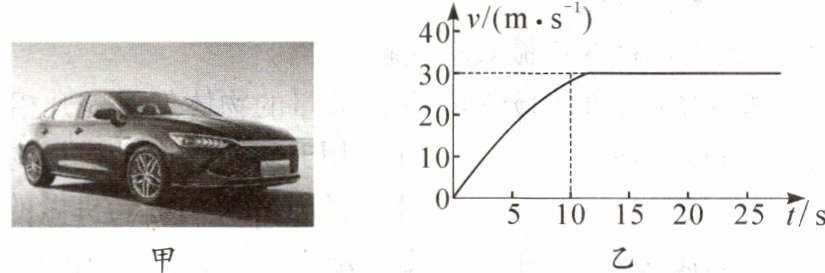
10. 随着人们生活水平不断提高,小龙家最近也买了辆轿车(如图甲)。若轿车以90 kW的恒定功率启动做直线运动,运动过程中受到的阻力不变,运动的速度v与时间t的关系如图乙所示,则经过10 s轿车发动机所做的功是9×10^{5}J,当牵引力为3×10^{3}N时轿车能保持匀速直线运动。

答案： 【解析】：
本题可根据功率公式$P = \frac{W}{t}$计算轿车发动机所做的功，再结合轿车匀速直线运动时的受力平衡求出牵引力。
步骤一：计算经过$10s$轿车发动机所做的功
已知轿车的功率$P = 90kW = 90×10^{3}W$，运动时间$t = 10s$。
根据功率的计算公式$P=\frac{W}{t}$（其中$P$为功率，$W$为功，$t$为时间），变形可得$W = Pt$。
将$P = 90×10^{3}W$，$t = 10s$代入$W = Pt$，可得：
$W=90×10^{3}W×10s = 9×10^{5}J$。
步骤二：计算轿车能保持匀速直线运动时的牵引力
由$v - t$图像可知，轿车在$10s$后做匀速直线运动，此时速度$v = 30m/s$。
根据功率公式$P = Fv$（其中$P$为功率，$F$为牵引力，$v$为速度），变形可得$F=\frac{P}{v}$。
将$P = 90×10^{3}W$，$v = 30m/s$代入$F=\frac{P}{v}$，可得：
$F=\frac{90×10^{3}W}{30m/s}=3×10^{3}N$。
因为轿车做匀速直线运动时，牵引力与阻力是一对平衡力，大小相等，所以当牵引力为$3×10^{3}N$时轿车能保持匀速直线运动。
【答案】：
$9×10^{5}$；$3×10^{3}$

11. 小李同学想利用所学的物理知识估测自己跳绳时克服重力的平均功率(不计绳重)。
(1)实验需要测量的物理量：
①用台秤(填测量器材)测量自己的质量m；
②测自己平均每次跳起的高度h(人的重心上升的高度)；
③用秒表(填测量器材)记录跳n次绳所用的时间t(填物理量与其对应字母)。
(2)跳绳时平均功率表达式P=$\frac{nmgh}{t}$(用以上的字母和g表示)。

(3)为计算方便,若小李的质量m= 50 kg,他跳绳时的重心高度随时间变化的情况如图所示,根据所给条件可估算出他每跳一次克服重力所做的功是25J,在1 min内克服重力做功的平均功率为75W。(g取10 N/kg)
(4)小李想和吴哥比较跳绳的平均功率(假设两人跳起的平均高度相同),则A(填选项)。
A. 频率相同,体重大的功率大
B. 频率相同,跳的时间长的功率大
C. 体重相同,频率高的功率小
D. 体重相同,跳的时间长的功率大

答案：
(1)①台秤；③秒表；时间t
(2)$\frac{nmgh}{t}$
(3)25；75
(4)A

12. 【前沿科技】2024年11月13日,在珠海航展兵器馆亮相的“机器狼”受到观众喜爱,成为名副其实的明星展品。如图所示,机器狼的质量为20 kg,在水平地面上匀速行走时受到的阻力是总重的0.2倍,某次展示时,机器狼以10.8 km/h的速度匀速前进30 s到达预定地点后四足站立对周围进行侦查,g取10 N/kg。求：

(1)这次展示机器狼移动的距离。
(2)机器狼水平匀速前进过程的功率。

答案： 【解析】：
本题主要考查速度公式和功率公式的应用。
（1）首先需要将机器狼的速度从$km/h$转换为$m/s$，然后利用速度公式$s = vt$计算出机器狼移动的距离。
（2）需要先计算出机器狼受到的阻力，由于机器狼是匀速前进的，所以其受到的牵引力等于阻力。然后利用功率公式$P = Fv$计算出机器狼水平匀速前进过程的功率。
【答案】：
(1)解：机器狼的速度$v = 10.8km/h = 3m/s$，
机器狼移动的距离：$s = vt = 3m/s × 30s = 90m$；
综上所述，答案为：这次展示机器狼移动的距离为$90m$。
(2)解：机器狼的重力：$G = mg = 20kg × 10N/kg = 200N$，
机器狼匀速行走时受到的阻力：$f = 0.2G = 0.2 × 200N = 40N$，
因为机器狼匀速前进，所以牵引力$F = f = 40N$，
机器狼水平匀速前进过程的功率：$P = Fv = 40N × 3m/s = 120W$。
综上所述，答案为：机器狼水平匀速前进过程的功率为$120W$。