《2025年超越训练八年级数学上册人教版四川专版》

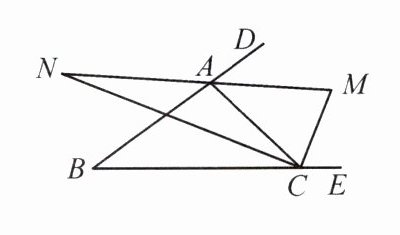
10. 如图，$\triangle ABC$的外角$\angle DAC$和$\angle ECA$的平分线相交于点$M$，$MA$的延长线与$\angle ACB$的平分线相交于点$N$.若$\angle M = 4\angle N$，求$\angle B$的度数.

答案： 10.解:
∵CN平分∠ACB,AM平分∠DAC,
∴∠ACN=$\frac{1}{2}$∠ACB,∠MAC=$\frac{1}{2}$∠DAC.
∵∠N+∠ACN=∠MAC=$\frac{1}{2}$∠DAC,
∴2∠N+∠ACB=∠DAC.又∠B+∠ACB=∠DAC,
∴2∠N=∠B,即∠N=$\frac{1}{2}$∠B.
∵∠NCM=∠ACN+∠ACM=$\frac{1}{2}$(∠ACB+∠ACE)=90°,
∴∠M+∠N=90°,
∴∠M=90°−$\frac{1}{2}$∠B.
∵∠M=4∠N,
∴90°−$\frac{1}{2}$∠B=4×$\frac{1}{2}$∠B,解得∠B=36°.

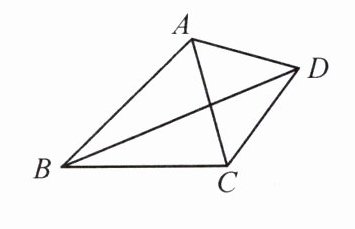
11. 如图，在四边形$ABCD$中，$BD$平分$\angle ABC$，$\angle BAD + \angle CAD = 180^{\circ}$，$\angle BCD + \angle ACD = 180^{\circ}$.
(1)若$\angle ABC = 44^{\circ}$，求$\angle ADC$的度数.
(2)若$\angle BAC = 62^{\circ}$.①$\angle BDC$的度数是31°；②求$\angle ACD - \angle ABD$的度数.

答案：
11.解:
(1)如图,分别延长BA,BC至点E,F.
∵∠BAD+∠CAD=180°,∠BAD+∠EAD=180°,
∴∠CAD=∠EAD,即AD平分∠EAC.同理可得CD平分∠FCA，
∴∠ADC=90°−$\frac{1}{2}$∠ABC=90°−$\frac{1}{2}$×44°=68°.
(2)①31°.
②
∵∠BAC+∠ABD=∠BDC+∠ACD,
∴∠ACD−∠ABD=∠BAC−∠BDC=31°.

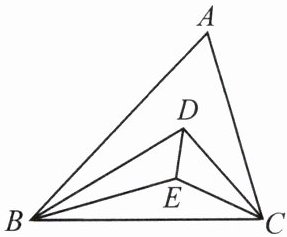
12. 如图，在$\triangle ABC$中，$\angle ABC$，$\angle ACB$的三等分线交于点$D$，$E$.
（1）求证：$\angle BEC = 120^{\circ} + \frac{1}{3}\angle A$；
（2）连接$DE$，若$\angle A = 60^{\circ}$，求$\angle BDE$的度数.

答案： 12.
(1)证明:
∵∠ABC,∠ACB的三等分线交于点E,
∴∠EBC=$\frac{1}{3}$∠ABC,∠ECB=$\frac{1}{3}$∠ACB,
∴∠BEC=180°−(∠EBC+∠ECB)=180°−$\frac{1}{3}$(∠ABC+∠ACB)=180°−$\frac{1}{3}$(180°−∠A)=120°+$\frac{1}{3}$∠A.
(2)解:同
(1)可得∠BDC=180°−$\frac{2}{3}$(∠ABC+∠ACB)=180°−$\frac{2}{3}$×(180°−60°)=100°.
∵BE,CE分别平分∠DBC,∠DCB,
∴DE平分∠BDC,
∴∠BDE=$\frac{1}{2}$∠BDC=$\frac{1}{2}$×100°=50°.