4. 如图,在 $\triangle ABC$ 中,$BD$,$CE$ 分别是 $AC$,$BC$ 边上的高.
(1) 若 $\angle A = 60^{\circ}$,则 $\angle BOC =$


(1) 若 $\angle A = 60^{\circ}$,则 $\angle BOC =$
120°
;(2) 若 $\angle A = \alpha$,则 $\angle BOC =$ 180°- \alpha
.


答案:
$4.(1)120° (2)180°- \alpha$
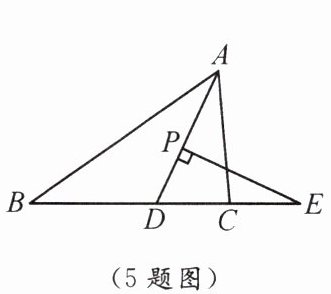
5. 如图,在 $\triangle ABC$ 中,$AD$ 平分 $\angle BAC$,$P$ 为线段 $AD$ 上一点,$PE \perp AD$ 交 $BC$ 的延长线于点 $E$. 若 $\angle B = 35^{\circ}$,$\angle ACB = 85^{\circ}$,则 $\angle E$ 的度数是
25°
.
答案:
5.25°
6. 如图,在 $\triangle ABC$ 中,$\angle ABC = \angle ACB$,$CD \perp AB$,垂足为 $D$.
(1) 若 $\angle A = 40^{\circ}$,则 $\angle BCD$ 的度数是
(1) 若 $\angle A = 40^{\circ}$,则 $\angle BCD$ 的度数是
20°
;(2) 若 $\angle A = \alpha$,则 $\angle BCD$ 的度数是 \frac{\alpha}{2}
.
答案:
$6.(1)20° (2)\frac{\alpha}{2}$
7. 如图,在 $\triangle ABC$ 中,$\angle BAC : \angle ABC : \angle C = 7 : 8 : 3$,$AD \perp BC$,$BE \perp AC$,垂足分别为 $D$,$E$,$BE$ 与 $AD$ 相交于点 $H$,求 $\angle EHD$ 的度数.


答案:
7.解:设$ \angle BAC = 7x, \angle ABC = 8x, \angle C = 3x,$则$ \angle BAC + \angle ABC + \angle C = 7x + 8x + 3x = 180°,$解得 x = 10°,$\therefore \angle C = 3x = 30°.\because AD \perp BC,$$\therefore \angle DAC = 90° - \angle C = 60°.\because BE \perp AC,$$ \therefore \angle AEH = 90°,$$\therefore \angle EHD = \angle DAC + \angle AEH = 60° + 90° = 150°.$
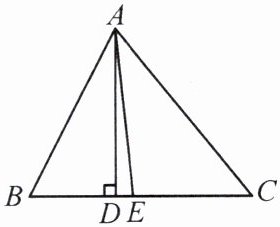
8. 如图,在 $\triangle ABC$ 中,$AD \perp BC$,垂足为 $D$,$AE$ 平分 $\angle BAC$.
(1) 若 $\angle B = 63^{\circ}$,$\angle C = 51^{\circ}$,求 $\angle DAE$ 的度数;(2) 若 $\angle B - \angle C = 10^{\circ}$,求 $\angle DAE$ 的度数.
(1) 若 $\angle B = 63^{\circ}$,$\angle C = 51^{\circ}$,求 $\angle DAE$ 的度数;(2) 若 $\angle B - \angle C = 10^{\circ}$,求 $\angle DAE$ 的度数.

答案:
8.解:$(1) \because \angle BAC = 180° - \angle B - \angle C,$AE 平分$ \angle BAC,$$ \therefore \angle BAE = \frac{1}{2} \angle BAC = 90° - \frac{1}{2} \angle B - \frac{1}{2} \angle C.\because AD \perp BC,$$ \therefore \angle BAD = 90° - \angle B,$$\therefore \angle DAE = \angle BAE - \angle BAD = 90° - \frac{1}{2} \angle B - \frac{1}{2} \angle C - (90° - \angle B) = \frac{1}{2} (\angle B - \angle C) = 6°.(2)$由
(1)可得$ \angle DAE = \frac{1}{2} (\angle B - \angle C) = 5°.$
(1)可得$ \angle DAE = \frac{1}{2} (\angle B - \angle C) = 5°.$
9. 如图,在 $\triangle ABC$ 中,$\angle BAC = \angle B$,$AD \perp BC$,垂足为 $D$,$AE$ 平分 $\angle DAC$ 交 $CD$ 于点 $E$,$EF \perp AB$,垂足为 $F$,求 $\angle AEF$ 的度数.


答案:
9.解:$\because AE $平分$ \angle DAC,$$\therefore $设$ \angle DAE = \angle EAC = x.\because AD \perp BC,$$ \therefore \angle C = 90° - \angle DAC = 90° - 2x.$又$ \angle BAC = \angle B,$$\therefore \angle BAC = \frac{1}{2} (180° - \angle C),$即$ \angle BAC = \frac{1}{2} (180° - 90° + 2x) = 45° + x,$$ \therefore \angle FAE = \angle BAC - \angle EAC = 45° + x - x = 45°.\because EF \perp AB,$$ \therefore \angle AEF = 90° - \angle FAE = 45°.$
查看更多完整答案,请扫码查看


