7. 如图,在等边三角形 $ABC$ 中,$P$ 是边 $BC$ 上一点,$PM \perp AB$ 于点 $M$,$PN \perp AC$ 于点 $N$,试说明 $\triangle AMN$ 与四边形 $BMNC$ 的周长之间的关系.


答案:
7.解:设$BM=a$,$CN=b$,易得$\angle BPM=\angle CPN=30^{\circ}$,$\therefore PB=2BM=2a$,$PC=2CN=2b$,$\therefore AB=AC=BC=2a+2b$,$\therefore AM=a+2b$,$AN=2a+b$,$\therefore C_{\triangle AMN}=AM+AN+MN=a+2b+2a+b+MN=3a+3b+MN$,$C_{四边形BMNC}=MB+BC+NC+MN=a+2a+2b+b+MN=3a+3b+MN$,$\therefore C_{\triangle AMN}=C_{四边形BMNC}$ ,即$\triangle AMN$,与四边形$BMNC$,的周长相等。
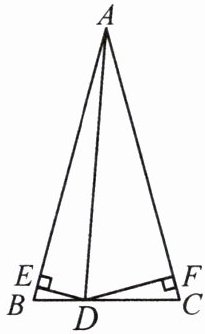
8. 如图,在 $\triangle ABC$ 中,$AB = AC$,$\angle BAC = 30^{\circ}$,$D$ 为 $BC$ 边上一点,$DE \perp AB$ 于点 $E$,$DF \perp AC$ 于点 $F$.若 $DE + DF = \frac{7}{3}$,求 $AB$ 的长.

答案:
8.解:如图,过点$B$作$BM\perp AC$于点$M$。$\because S_{\triangle ABD}+S_{\triangle ACD}=S_{\triangle ABC}$,$\therefore\frac{1}{2}AB\cdot DE+\frac{1}{2}AC\cdot DF=\frac{1}{2}AC\cdot BM$。$\because AB=AC$,$\therefore BM=DE+DF=\frac{7}{3}$。又$\angle BAC=30^{\circ}$,$\therefore AB=2BM=\frac{14}{3}$。

8.解:如图,过点$B$作$BM\perp AC$于点$M$。$\because S_{\triangle ABD}+S_{\triangle ACD}=S_{\triangle ABC}$,$\therefore\frac{1}{2}AB\cdot DE+\frac{1}{2}AC\cdot DF=\frac{1}{2}AC\cdot BM$。$\because AB=AC$,$\therefore BM=DE+DF=\frac{7}{3}$。又$\angle BAC=30^{\circ}$,$\therefore AB=2BM=\frac{14}{3}$。

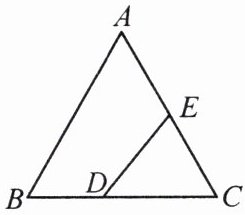
9. 如图,在等边三角形 $ABC$ 中,$AB = 6$,$E$ 为 $AC$ 的中点,$D$ 为边 $BC$ 上一动点,连接 $DE$,求 $DE + \frac{1}{2}BD$ 的最小值.

答案:
9.解:如图,连接$BE$,以$BE$为边在其下方作等边三角形$BEF$,$EF$交$BC$于点$H$。过点$D$作$DN\perp BF$于点$N$,过点$E$作$EM\perp BF$于点$M$。

易得$BC$与$EF$垂直,设$BC\perp EF$于点$H$。$\because E$为$AC$的中点,$\therefore\angle EBC=\frac{1}{2}\angle ABC=30^{\circ}$。
$\because\triangle BEF$为等边三角形,$\therefore\angle FBC=30^{\circ}$,$\therefore DN=\frac{1}{2}BD$,$\therefore DE+\frac{1}{2}BD=DE+DN\geqslant EM$,即$DE+\frac{1}{2}BD$的最小值为$EM$的长。在$\triangle BHE$和$\triangle EMB$中,$\begin{cases} \angle BHE=\angle EMB=90^{\circ},\\ \angle BEH=\angle EBM=60^{\circ},\\ BE=EB,\end{cases}$
$\therefore\triangle BHE\cong\triangle EMB(AAS)$,$\therefore EM=BH$,$\therefore DE+\frac{1}{2}BD$的最小值为$BH$的长。$\because CH=\frac{1}{2}CE=\frac{3}{2}$,$BH=BC - CH=6-\frac{3}{2}=\frac{9}{2}$,$\therefore DE+\frac{1}{2}BD$的最小值为$\frac{9}{2}$。
9.解:如图,连接$BE$,以$BE$为边在其下方作等边三角形$BEF$,$EF$交$BC$于点$H$。过点$D$作$DN\perp BF$于点$N$,过点$E$作$EM\perp BF$于点$M$。

易得$BC$与$EF$垂直,设$BC\perp EF$于点$H$。$\because E$为$AC$的中点,$\therefore\angle EBC=\frac{1}{2}\angle ABC=30^{\circ}$。
$\because\triangle BEF$为等边三角形,$\therefore\angle FBC=30^{\circ}$,$\therefore DN=\frac{1}{2}BD$,$\therefore DE+\frac{1}{2}BD=DE+DN\geqslant EM$,即$DE+\frac{1}{2}BD$的最小值为$EM$的长。在$\triangle BHE$和$\triangle EMB$中,$\begin{cases} \angle BHE=\angle EMB=90^{\circ},\\ \angle BEH=\angle EBM=60^{\circ},\\ BE=EB,\end{cases}$
$\therefore\triangle BHE\cong\triangle EMB(AAS)$,$\therefore EM=BH$,$\therefore DE+\frac{1}{2}BD$的最小值为$BH$的长。$\because CH=\frac{1}{2}CE=\frac{3}{2}$,$BH=BC - CH=6-\frac{3}{2}=\frac{9}{2}$,$\therefore DE+\frac{1}{2}BD$的最小值为$\frac{9}{2}$。
查看更多完整答案,请扫码查看


