《2025年超越训练八年级数学上册人教版四川专版》

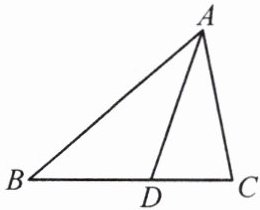
2. 如图，在$\triangle ABC$中，$AD$平分$\angle BAC$，$AB = 9$，$AC = 6$，$BC = 8$。求：
(1)$\triangle ABD$与$\triangle ACD$的面积比值；
(2)$\triangle ABD$与$\triangle ACD$的周长差。

答案：
2.解:
(1)如图,过点D作DM⊥AB于点M,DN⊥AC于点N.
∵AD平分∠BAC,且∠AMD=∠AND=90°,AD=AD,
∴△ADM≌△ADN(AAS),
∴DM=DN,
∴$\frac{S_{\triangle ABD}}{S_{\triangle ACD}} = \frac{\frac{1}{2}AB\cdot DM}{\frac{1}{2}AC\cdot DN} = \frac{AB}{AC} = \frac{9}{6} = \frac{3}{2}$.
(2)由
(1)知,$\frac{S_{\triangle ABD}}{S_{\triangle ACD}} = \frac{3}{2}$.
∵$\frac{S_{\triangle ABD}}{S_{\triangle ACD}} = \frac{BD}{CD}$，
∴$\frac{BD}{CD} = \frac{3}{2}$，
∴$BD = \frac{3}{5}BC = \frac{24}{5}$，$CD = \frac{2}{5}BC = \frac{16}{5}$，
∴$C_{\triangle ABD} - C_{\triangle ACD} = AB + BD + AD - (AC + CD + AD) = AB + BD - AC - CD = \frac{23}{5}$.

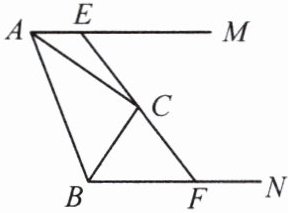
3. 如图，$AM// BN$，$\angle MAB$与$\angle NBA$的平分线相交于点$C$，过点$C$的一条直线分别与$AM$，$BN$相交于$E$，$F$两点。求证：$AB = AE + BF$。

答案：
3.证明:
∵AM//BN,AC,BC分别平分∠MAB,∠NBA,
∴∠CAB+∠CBA=$\frac{1}{2}$(∠MAB+∠NBA)=$\frac{1}{2}$×180°=90°,
∴∠ACB=90°.如图,延长BC交AM于点D.
∵∠DAC=∠BAC,AC=AC,∠ACB=∠ACD=90°,
∴△ACB≌△ACD (ASA),
∴CB=CD,AB=AD=AE+DE.
∵AM//BN,
∴∠FBC=∠EDC.又∠BCF=∠DCE,CB=CD,
∴△BCF≌△DCE(ASA),
∴DE=BF,
∴AB=AE+DE=AE+BF.

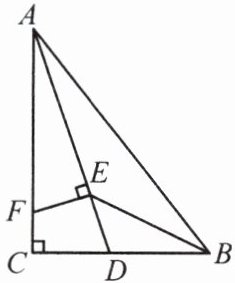
4. 如图，在$\triangle ABC$中，$\angle C = 90^{\circ}$，$\angle BAC$的平分线$AD$交$BC$于点$D$，$BE$平分$\angle ABC$交$AD$于点$E$，$FE\perp AD$交$AC$于点$F$。
(1)求$\angle BED$的度数；
(2)求证：$AB = AF + BD$。

答案：
4.
(1)解:
∵AE,BE分别平分∠BAC,∠ABC,∠C=90°,
∴∠AEB=90°+$\frac{1}{2}$∠C=135°,
∴∠BED=180°−∠AEB=45°.
(2)证明:如图,延长FE交AB于点G.
∵FE⊥AD,
∴∠AEF=∠AEG=90°.又∠FAE=∠GAE、AE=AE,
∴△AEF≌△AEG(ASA),
∴AG=AF.
∵∠BED=45°,∠DEG=90°,
∴∠BEG=∠BED=45°.又∠EBD=∠EBG,BE=BE,
∴△BED≌△BEG(ASA),
∴BG=BD,
∴AB=AG+BG=AF+BD.